Выходные данные
УДК 661.24
Рецензенты:
доктор геолого-минералогических наук Л.Э.Левин,
доктор геолого-минералогических наук Б.А. Соколов
Печатается по постановлению
Редакционно-издательского совета Московского университета
Зоненшайн Л.П., Ломизе М.Г., Рябухин А.Г.
Пособие к практическим занятиям по геотектонике
Учебное пособие. – М.; Изд-во МГУ, 1990. – 95 с.
ISBN 5-211-01969-5
В учебном пособии рассматриваются наиболее распространенные задачи, применяемые геологами при тектонических исследованиях. Разбираются методы изучения вертикальных и горизонтальных движений, расчета движения литосферных плит при палинспастических реконструкциях. Показаны приемы составления тектонических, в том числе геодинамических, карт разного масштаба. В приложении даны программы для расчета на ЭВМ параметров относительного движения литосферных плит.
Для студентов геологических специальностей и специалистов, занимающихся вопросами тектоники.
Введение
Последние годы геотектоника преподается студентам геологических специальностей по новой учебной программе, отражающей коренные изменения, произошедшие в этой области геологии. Учебный курс построен на актуалистическом подходе к решению задач геотектоники, большое внимание уделяется новым методам исследования. Поскольку на практических занятиях могут быть рассмотрены лишь некоторые из них, авторы пособия стояли перед необходимостью отобрать наиболее важные темы, в том числе нуждающиеся в практической проработке. Поэтому только небольшая часть пособия посвящена традиционным вопросам, таким как применение метода фаций и мощностей, составление тектонических карт обычного типа. Остальное место отведено методам определения шарьяжных и сдвиговых перемещений, расчету параметров движения литосферных плит, палеомагнитным методам палинспастических реконструкций, составлению геодинамических карт. В приложении приведены компьютерные программы для расчета и решения основных задач тектоники литосферных плит.
Учебное пособие подготовлено на кафедре динамической геологии геологического факультета МГУ. Работа велась в творческом содружестве с сотрудниками лаборатории палеогеодинамики ИО АН СССР. Первые три раздела главы 1 и глава 3 написаны М.Г. Ломизе‚ четвертый раздел главы 1 и глава 2 – Л.П. Зоненшайном и А.Г. Рябухиным. Программы составлены М.В.Кононовым и Н.Ю.Бочаровой.
Авторы благодарны кандидату геолого-минералогических наук В.Н. Вадковскому за ценные замечания, сделанные при предварительном просмотре рукописи.
ГЛАВА 1. Изучение тектонических движений
Любое геологическое тело участвует в разнообразных тектонических движениях, которые могут быть замечены и измерены относительно других частей литосферы, а иногда и по отношению к подлитосферной мантии. Отсчет вертикальной компоненты движений обычно ведут от уровня Мирового океана; по возможности учитывают эвстатические изменения этого уровня. Некоторые параметры крупных горизонтальных перемещений (вращение, изменение палеошироты) могут быть определены относительно геомагнитных полюсов.
Только самые быстрые "сейсмогенные" движения доступны непосредственному наблюдению. При этом наибольшее значение имеет решение фокального механизма очагов землетрясений (по первым вступлениям сейсмических волн), которое дает ориентировку главных осей напряжения, а с учетом геологических данных – и направление относительного смещения в очаге. Во всех остальных случаях мы судим о тектонических движениях главным образом по начальному и конечному положению движущихся геологических тел за определенный отрезок времени. Для современных движений это достигается в основном геодезическими и другими инструментальными методами, в том числе повторными промерами расстояний между удаленными объектами, которые стали возможны благодаря радиоинтерферометрии и спутниковым лазерным отражателям. Для движений неоген-четвертичного времени ("новейших движений") велика роль геоморфологических методов. Для остальной геологической истории информация о тектонических движениях заключена в составе, форме и размещении геологических тел, в их седиментационной и деформационной структуре, в нарушениях их первоначального и последующего взаимного размещения, в палеомагнитных данных. Для позднего мезозоя-кайнозоя важны также возрастная зональность (линейные магнитные аномалии) океанского дна и его разрывная тектоника.
На практических занятиях знакомятся с некоторыми из наиболее важных методов.
Изучение вертикальных движений методом фаций и мощностей
Метод фаций и мощностей – один из традиционных методов геотектоники – особенно широко применяется при геологическом обеспечении нефте- и газопоисковых работ на платформах, в межгорных и передовых прогибах, а также на континентальных окраинах. Он дает количественную или полуколичественную оценку вертикальных движений (опусканий и относительных поднятий) в древних бассейнах седиментации. Величина перемещения за взятый отрезок времени в заданной точке получается как сумма двух слагаемых: мощности накопившихся осадков и изменения глубины бассейна, о котором судят по фациальнкм признакам. В зависимости от конкретных условий ошибка определения каждого из этих слагаемых варьирует в широких пределах.
Распределение мощностей отложений (в изолиниях мощности – изопахитах) и размещение фаций (обозначенных окраской или штриховыми знаками) обычно даются на одной карте. Как правило, на исследуемую территорию составляют серию карт для последовательных стратиграфических единиц: это позволяет судить о развитии вертикальных тектонических движений и создаваемых ими прогибов и поднятий.
Исходными материалами на практическом занятии служат карта точек наблюдений и таблица, где для каждой точки дана полная (не искаженная последующим размывом) мощность отложений и их фациальная характеристика. Даются сведения и о тех точках, в которых отложения соответствующего возраста изначально отсутствовали: по ним оконтуриваются "области нулевых мощностей", т.е. области относительного поднятия и денудации.
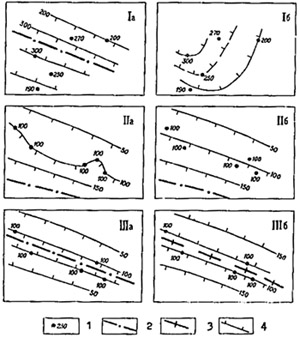
Рис. 1. Некоторые случаи проведения изопахит на карте мощностей отложений.
1 – проведение изопахит в случае линейно вытянутых прогибов и поднятий: Iа – правильное построение карты, намечены оси прогибов и поднятий с учетом их простирания, затем проведены изопахиты с интерполяцией раздельно на каждом склоне, Iб – неправильное проведение изопахит посредством свободной интерполяции между всеми точками наблюдения? II – варианты проведения изопахит без учета (IIа) и с учетом (IIб) специфики исходных данных (см. текст); III – примеры проведения изопахит вблизи оси прогибов (IIIа) и поднятий (IIIб).
1 – точки наблюдения и мощности, м; 2 – оси прогибов 3 – оси поднятий; 4 – изопахиты (штрихи – в сторону нарастания мощностей)
Проведение изопахит для более или менее изометричных платформенных прогибов с невысокими градиентами мощностей производится путем обычной интерполяции между заданными точками наблюдения. Однако в случае линейно вытянутых прогибов такое построение изопахит может привести к грубым ошибкам, при этом необходимо учитывать господствующее простирание прогибов, о котором можно судить по ориентировке линейной складчастости на геологической карте. Рекомендуется сначала наметить оси прогибов и поднятий, а затем провести изопахиты на их склонах (рис. 1,1а).
На рис. 1,1б по тем же исходным данным, что и на предыдущем рисунке, дана вполне строгая интерполяция, но без учета дополнительных сведений о линейности прогиба и его простирании. Поэтому здесь интерполяция производилась и между точками, находящимися на противоположных бортах прогиба, а полученная в результате карта изопахит геологически неверна.
При проведении изопахит не следует забывать о размерах погрешности используемых определений мощности, а также о том, что местоположение точек наблюдения (естественных обнажений, скважин, горных выработок) зависит от многих разнообразных причин и по отношению к изопахитам является случайным. На рис. 1.II даны два варианта проведения изопахит по одним и тем же данным. Поскольку обычно используются округленные (или приблзиительные) значения мощности, второй вариант более правильный. На рис. 1.III приведены примеры проведения изопахит вблизи осей прогибов и поднятий. При необходимости особым знаком показываются изопахиты половинного или более дробного сечения.
При проведении границ между фациями (или фациальными зонами) обычно исходят из сопряженности этих границ с неровностями тектонического рельефа в бассейне седиментации и с размещением мощностей. Поэтому необходимо по возможности согласовывать фациальные границы с изопахитами.
Если для одной территории составляется последовательная серия карт фаций и мощностей, то нужно согласовывать и смежные карты такой серии. Нередко это позволяет выбрать наилучший вариант проведения изопахит и фациальных границ.
При анализе серии карт фаций и мощностей основное внимание уделяется размещению прогибов и поднятий, их развитию во времени: изменению границ миграции, переориентировке и т.д. Наглядную помощь могут оказать профили через карту фаций и мощностей (так называемые "фациальные профили"), особенно серии таких профилей. построенных по одной линии для последовательных отрезков времени. Если прогибы и поднятия линейны, то профили проводят вкрест их простирания. Вертикальный масштаб обычно берется преувеличенным относительно горизонтального.
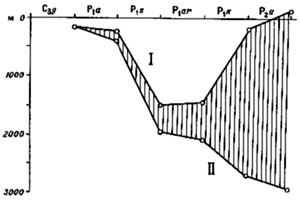
Рис. 2. Построение графика вертикальных тектонических движений для заданной точки по данным о глубинах бассейна седиментации, и о мощностях отложений.
I – линия вертикальных перемещений поверхности осадков; II – линия вертикальных тектонических движений
Анализу серии карт фаций и мощностей способствует в построение графиков вертикальных тектонических движений для некоторых представительных точек. Наиболее информативны точки, находящиеся в центральной части прогибов. Такие графики обычно строят, откладывая по горизонтали геологическое время (в условных или абсолютных единицах), а по вертикали – глубины бассейна – глубины бассейна сеиментации (положение поверхности осадков в бассейне седиментации относительно уровня моря) и мощности отложений (рис. 2). На графике верхняя линия наглядно изображает вертикальные перемещения поверхности осадков, нижняя – собственно тектонические движения (вертикальные) за время седиментации. Наибольшую трудность при построении таких графиков представляет количественная оценка глубин бассейна седиментации по фациальным признакам отложений.
На практических занятиях значения глубин бассейна либо должны быть указаны в задании, либо, если график строится по серии карт фаций и мощностей, необходимо условиться об определенной оцифровке глубин формирования каждой фации.
Если есть возможность оперировать абсолютными датировками отложений, то при анализе карт фаций и мощностей учитываются и скорости вертикальных движений: их различие на разных участках территории и изменение во времени. Могут быть построены графики изменения скорости вертикальных движений для наиболее показательных точек.
На практических занятиях по данному разделу могут быть использованы "Атлас литолого-палеогеографических карт Русской платформы" масштаба 1:5000000 (редактор А.П. Виноградов) и "Атлас литолого-палеогеографических карт СССР" масштаба 1:7500000 (редакторы А.Б. Ронов и В.Е. Хаин).
Определение шарьяжных перемещений с учетом анализа фаций
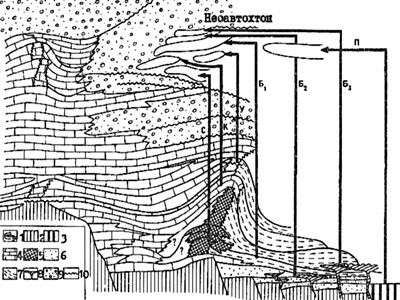
Рис. 3. Первоначальное размещение и последовательные шарьяжные перемещения фациальных комплексов палеозоя в Уфимском амфитеатре (Средний Урал) (по А.Е. Живковичу н П.А.Чеховичу).
1 – тектоническое перемещение (шарьирование): 2,3 – породы основания: 2 – осадочные и метаосадочные, 3 – основные и ультраосновные; 4 – 9 – фациальные комплексы: 4 – эпиконтинентальных шельфовых морей и внутреннего шельфа, 5 – карбонатные шельфовой окраины, 6 – терригенные ранней стадии развития окраины, 7 – континентального склона и его подножья, 8 – вулканогенные, 9 – орогенные молассы; 10 – важнейшие несогласия. Параавтохтоны: С – Сергинский, К – Каменско-Демидский, У – Уткинский. Аллохтоны: Б – Бердымо-Киргишанский (Б1 – нижняя пластина, Б2 – зона меланжа, Б3 – верхняя пластина), П – Полуденский (офиолитовый)
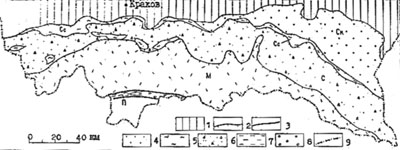
Рис. 4. Размещение фациальных комплексов верхнего сенона в современной покровно-складчатой структуры Западных Карпат (Геологический атлас Польши, по К.Биркенмайеру и др.)
1 – платформа и передовой прогиб; 2 – надвиги на границе тектонических покровов: Скольского (Cк), Субсилезского (Cс), Силезского (С) Магурского (М); 3 – крутые разломы, ограничивающие Пьенинскую утесовую зону (П); 4 – 8 – фациальные комплексы; 4 – иноцерамовые слои (песчаники), 5 – венгловецкие пестрые мергели, 6 – нижние истебнянские слои (песчаники, глинистые сланцы, олистостромы); 7 – пуховские красные мергели; 8 – ярмутские слои (конгломераты, песчаники); 9 – государственные границы
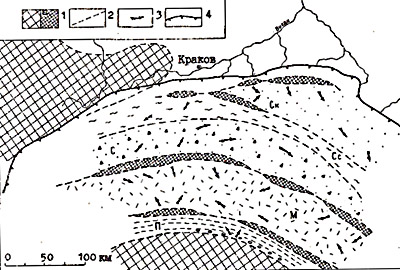
Рис. 5. Палинспастичeская реконструкция для позднего сенона Западных Карпат (Геологический атлас Польши, по К.Биркенмайеру и др.)
1 – области размыва, в том числе кордильеры (а); 2 – границы фациальных комплексов; 3 – направление переноса осадочного материала; 4 – фронт карпатских шарьяжей. Остальные обозначения см. на рис. 4
Определение величины горизонтальных перемещений при формировании шарьяжей – трудная и не всегда разрешимая задача. Для каждого тектонического покрова ставится вопрос о величине смещения относительно его корней – той тектонической зоны или сутуры, откуда были выжаты породы аллохтона. Однако в покровноскладчатых сооружениях и эти корневые зоны могут испытывать горизонтальное смещение относительно других единиц континентальной коры, что усложняет задачу а затрудняет ее решение. Последняя сводится иногда к определению относительного перемещения аллохтонных единиц.
Структурные наблюдения над деформациями в основании тектонического покрова и его положение в региональной структуре позволяют судить о направлении шарьяжа. Размеры аллохтона дают указание на минимальную величину шарьирования. Более полное определение шарьяжных перемещений требует анализа фаций и реконструкции их первоначального взаимного размещения (рис. 3). Производится палинспастическая реконструкция, предусматривающая возвратное перемещение аллохтонннх единиц к месту формирования соответствующих фациальных комплексов в древнем бассейне седиментации. При реконструкции некоторая площадь отводится и тектоническим поднятиям, о них судят по продуктам размыва и по направлению переноса этого материала (рис. 4,5).
Во многих случаях при шарьяжных перемещениях нарушается первоначальная латеральная последовательность фаций: аллохтон может бить переброшен через соседнюю фациалъную зону, верхние покровные единицы могут опередить в процессе перемещения более низкие единицы аллохтона или пяравтохтона. Еще более сложная "перетасовка" фациальных комплексов происходит при повторных или многократных шарьяжных перемещениях. В таких случаях определение их величины тесно связано с задачей расшифровки первоначального относительного расположения фациальных комплексов (рис. 6).
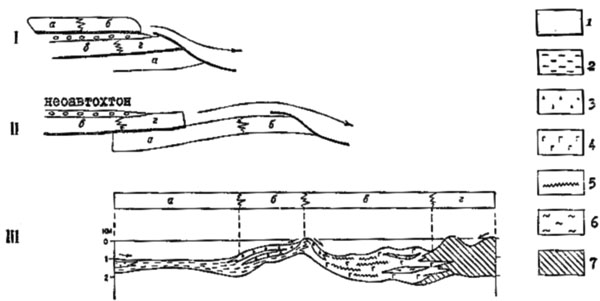
Палинспастическая реконструкция в условиях сложной покровной структуры, образовавшейся в результате двух этапов шарьирования, которые нарушили латеральную последовательность фациальных комплексов силура в Сакмарской зоне Южного Урала. Буквы на профилях – фациальные комплексы (по данным С.В.Руженцева)
На практических занятиях определение шарьяжных перемещений с учетом анализа фаций может быть рассмотрено на примере наиболее изученных покровно-складчатых сооружений, в том числе таких как Карпаты, Урал, Южный Тянь-Шань, Корякское нагорье.
Литература
Выявление региональных сдвигов, определение их направления и величины
Региональные сдвиги со смещением в единицы, десятки и сотни километров образуются как в континентальной коре, так и в океанах, где сдвиговые смещения обычно связаны с трансформными разломами. Нередко, особенно там, где сдвиги простираются параллельно геологическим границам они остаются незамеченными до проведения специальных наблюдений. Поэтому важно знание резких признаков сдвига, в том числе характерных приразяомаых деформаций на его крыльях, следов скольжения на поверхности сместителя. Эти признаки, а также решение фокальных механизмов для современных сейсмогенных сдвигов, позволяют определить наличие сдвигового смещения и его направление. Величина сдвига может быть определена только там, где он пересекает геологические (или геофизические) границы и структуры, и где удается распознать их смещенные части. Приблизительная величина сдвига иногда макет быть определена и по палеомагнитным данным – относительному вращению разделенных сдвигом литосферных единиц.
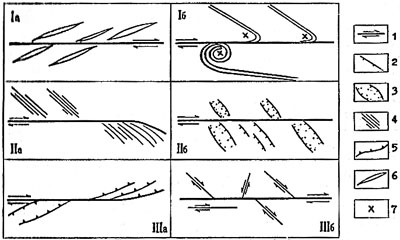
Рис. 7. Характерные деформации на крыльях сдвига (для случая правостороннего смещения) (по М.Г.Ломизе):
I – складки волочения: эшелонированные (кулисные) системы складок с горизонтальным шарниром (1а) и складки с вертикальным шарниром, в том числе структуры закручивания (1б); II – структуры растяжения: дайки и жилы по трещинам отрыва, в том числе системы типа "конского хвоста" (IIа); оперяющие сбросы и грабены (IIб); III – вторичные структуры скола: оперяющие взбросы и взбросо-надвиги, в том числе системы типа "конского хвоста" (IIIа); оперяющие сдвиги (IIIб).
1 – сдвиги; 2 – сбросы; 3 – грабены; 4 – дайки и жилы; 5 – взбросы и взбросо-надвиги; 6 – ось линейной складки в плане; 7 – то же, в поперечном сечении
При полевых работах исследуется поверхность сместителя разрыва: для сдвигов характерны зеркала скольжения с субгоризонтальными штрихами и бороздами, а также с уступами, которые ориентированы вкрест движению и обращены в сторону, обратную относительному перемещению наблюдаемого крыла разлома. Полевыми наблюдениями и методами микроструктурного анализа изучаются мелкие разрывные и пластические деформации в зоне сдвига, которые также указывают на его направление. Освоение этих методов – предмет структурной геологии, поэтому на практических занятиях по геотектонике основное внимание уделяется той информации о региональных сдвигах, которая может быть получена из геологических и структурных (или тектонических) карт главным образом крупного и среднего масштаба.
Это прежде всего системы разрывов и складок, формирующиеся на крыльях сдвига (рис. 7). Характерны складки волочения: эшелонированные (кулисно расположенные) складки с горизонтальными или пологонаклонными шарнирами, которые образуются в слоистых толщах на обрамлении сдвига при пологом залегании слоев и вытянуты под углом 15 – 25° к разлому в направлении относительного перемещения наблюдаемого его крыла. В случае крутого залегания и благоприятного простирания слои при сдвиге подворачиваются, образуя складки с вертикальными или крутонакнонными шарнирами или даже спиралевидные структуры закручивания.
В более массивных породах образуются оперяющие главный разлом разрывы, закономерно ориентированные в зависимости от направления сдвига. Это могут быть структуры растяжения, вытянутые под углом 40 – 45° к главному разлому в направлении, обратном относительному перемещению наблюдаемого его крыла: оперяющие сбросы и грабены, а также рои даек и системы гидротермальных жил, образовавшиеся по трещинам отрыва. Это также и вторичные структуры скола: оперяющие взбросы и взбросо-надвиги (под углом 15 – 25° к главному разлому в направлении относительного перемещения наблюдаемого крыла), оперяющие сдвиги нескольких определенных направлений (см.рис.7). В областях затухания сдвига гложет формироваться характерный структурный рисунок типа "конского хвоста". Для выявления региональных сдвигов полезно также знание их закономерной сопряженности (парагенеза) с другими региональными разломами и складчатыми структурами, которая выражена на геологических и тектонических картах соответствующими структурными рисунками. Примеры сдвигов приведены ка рис. 8 и 9.
 Рис. 10. Смещение пересекаемых разломом складок, позволяющее установить и измерить левосторонний сдвиг. Фудзино-Иманский разлом в Сихотэ-Алине (по В.Н.Силантьеву). |  Рис 11. Палинспастическая реконструкция с учетом смешения по Фудзино-Иманскому сдвигу, Сихотэ-Алинь (по В.Н.Силантьеву). |

Рис 8. Эшелонированная (кулиссообразная) система складок Главного Копетдагского разлома, указывающая на правосторонний сдвиг. (по Л.М.Расцветаеву)
1 – сдвиги; 2 – оси складок

Рис 9. Рои даек по системе трещин отрыва, оперяющих Южно-Алданский разлом (указывают на левосторонний сдвиг) (по Е.П.Гурову и Е.П.Гуровой, упрощено).
1 – сдвиг; 2 – рои даек
Величина сдвига может быть определена по геологической карте там, где он пересекает крутоориентированные границы геологических тел (в ттом числе интрузивные контакты, фациальные границы) или структурные формы (складки, разрывы). Если удается сопоставить и идентифицировать разобщенные и смещенные сдвигом части таких структур, то становится возможным измерить сдвиг и произвести палинспастическую реконструкцию путем возвратного горизонтального перемещения на карте крыльев разлома вплоть до совмещения частей рассеченного сдвигом геологического объекта (рис. 10, 11).
Литература
Движение плит и сферическая геометрия
Любое движение на сфере можно описать математически. Это в полной мере относится к перемещениям литосферных плит. При этом должны соблюдаться два условия (постулата) теории тектоники литосферных плит. Первый из них предполагает, что литосферные плиты являются жесткими, т.е. ведут себя как квазиупругие тела, способные передавать прилагаемые к ним напряжения на любые расстояния, не испытывая при этом внутренней деформации. Конечно, этот постулат оказывается справедливым в первом приближении (проведенные оценки жесткости плит показали, что плиты при их движении деформируются не более чем на первые проценты). Второй постулат говорит о неизменности радиуса Земли. Многие эмпирические данные и теоретические расчеты действительно показывают, что изменение радиуса Земли достигает не более сотых долей процента.
Если плиты представляют собой жесткие тела и движутся по сфере неизменного радиуса, то их движение описывается законами сферической геометрии. При расчетах перемещений литосферных плит используется теорема Эйлера, гласящая, что движение любого тела по поверхности сферы можно представить в виде вращения вокруг оси, проходящей через центр и пересекающей поверхности сферы двух точках, или полюсах. Самые простые рассуждения говорят о существ этой теоремы.
Представьте себе глобус. Перемещение любой точки на нем будет происходить не по прямой линии, а по дуге (Рис. 12) Если перемещение сложное, в виде изогнутой кривой, его всегда можно разложить на составные элементарные части, отвечающие каким-то конкретным малым дугам.
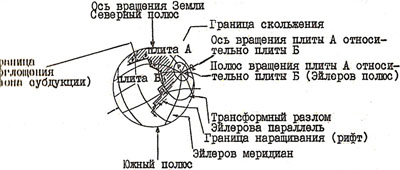
Рис 12. Схема движения плит А и Б на земной сфере
Можно представить литосферную плиту в виде сегмента тонкой сферической пленки, облекающей поверхность глобуса. Движения точек, составляющих пленку, будет происходить по концентрическим дугам, проведенным вокруг какой-то оси, проходящей через центр глобуса. Ось вращения пересекает поверхность сферы (глобуса) в двух точках антиподах, находящихся противоположных сторонах глобуса. Эти точки носят название Эйлеровых полюсов, или полюсов вращения. чем дальше находится данная точка от полюсов вращения, т.е. чем больше радиус дуги, тем больший путь при повороте на одинаковый угол она будет проходить по сравнению с другими точками, расположенными ближе к полюсу вращения.
Дуга, отстоящая на половине расстояния между полюсами вращения, т.е. на расстоянии 90° от каждого из них, является Эйлеровым экватором, отвечающим данной оси вращения, или данным полюсам вращения. Она представляет собой дугу большого круга. Остальные дуги, или Эйлеровы широты, отвечают малым окружностям, проведенным вокруг той же оси вращения.
Если мы хотим знать движение одной плиты по отношению к другой плите или по отношению к какой-либо точке на сфере, необходимо определить два главных параметра: положение полюса относительного вращения плит в виде его географических координат и величину поворота или угловую скорость движения (в градусах в год или в млн лет).
Определение этих параметров дает прямое и однозначное указание на то, какие события следует ожидать на границах плит: расходятся ли они, сходятся или скользят по отношению друг к другу. В идеальном случае определение параметров движения сравнительно просто: следует восстановить перпендикуляры к дугам, отвечающим движению плиты, и точка их пересечения даст положение полюса.
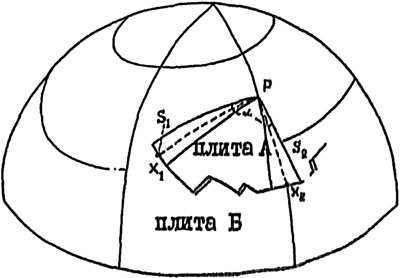
Рис. 13. Графическое определение параметров движения литосферных плит
Исходные данные. При количественных расчетах всегда используют конкретные данные, отражающие перемещения литосферных плит. Источники таких данных многообразны. Три из них являются количественными: кинематические, сейсмологические, палеомагнитные.
Кинематические данные включают, с одной стороны, измерения простираний трансформных разломов, сдвигов на континентах, линейных вулканических цепей в океанах как показателей направления движения плит, а с другой – расстояний между одновозрастными линейными магнитными аномалиями, находящимися по разные стороны от осей спрединга, как показателей скоростей движения плит.
Сейсмологические данные. Очерчивают современные границы литосферных плит и, кроме того, включают расчеты ориентировки напряжений в очагах землетрясений. Это позволяет определить азимут вектора смещения, отражающий направление относительного перемещения плит, что важно при вычислении параметров современных движений
Палеомагнитные данные получают при измерении остаточной намагниченности горных пород. Они позволяют определить положение в пространстве палеомагнитного вектора – его склонение по отношению к современному меридиану и наклонение по отношению к поверхности Земли. Исходя из этого, определяют положение палеомагнитных полюсов и палеошироты, намечают широтное перемещение плит или отдельных блоков земной коры (недостатком является невозможность установления долготной компоненты перемещения).
Качественные методы включают использование палеоклиматических данных (выделение комплексов – индикаторов прошлого климата), биогеографических данных, показывающих совмещение или разобщенность различных сообществ ископаемой фауны и флоры, геологических данных. Геологические данные важны для восстановления прошлого расположения границ литосферных плит. Они позволяют оценить распространение различных (в первую очередь магматических) комплексов-индикаторов границ литосферных плит и наметить положение самих границ. Например, пояса известково-щелочного вулканизма маркируют прошлые зоны субдукции; поля развития контрастного или бимодального, щелочного вулканизма позволяют очертить прошлые континентальные рифты; покровно-складчатые структуры, включающие офиолитовые покровы, меланжи и хаотические комплексы, отмечают положение зон континентального столкновения и др.
Изменение направлений движения плит
Существуют два основных метода установления направлений перемещения плит: по простираниям разломов сдвиговой природы и по ориентировке напряжений в очагах землетрясений.
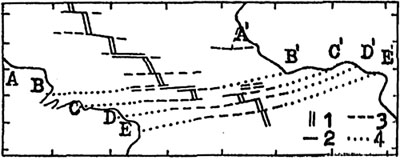
Рис. 14. Схема трансформных разломов Срединно-Атлантического хребта (по Дж.Вилсону).
1 – СОХ; 2 – активные разломы; 3 – след разлома, прекратившего развитие; 4 – гипотетическое продолжение разлома.
Если известно, что по разлому, разграничивающему две плиты, происходит "чистое" скольжение, то данный отрезок разлома совпадает с дугой окружности, проведенной из полюса относительного вращения двух плит. К числу таких разломов относятся трансформные разломы в океанах и сдвиги внутри континентов (например, разлом Сан-Андреас в Калифорнии или Альпийский разлом в Новой Зеландии). Необходимо в каких-то точках с установленными географическими координатами измерить простирания разлома (в виде азимутов простирания), и эти простирания будут отвечать направлению перемещения одной плиты относительно другой. При измерении простирания разломов неизбежно возникают погрешности из-за трудности точного фиксирования разломов на океанском дне (рис. 14).
Изменения азимутов простирания активных отрезков трансформных разломов, заключенных между двумя смещенными участками осевых зон срединных хребтов дают направления современных мгновенных перемещений плит. Простирание всего трансформного разлома в целом отвечает конечному вращению за время с начала возникновения данного разлома до современности. Полюса, вычисленные по коротким отрезкам трансформных разломов, можно рассматривать в качестве полюсов "мгновенного" вращения в определенные прошлые интервалы времени.
Кроме разломов, для определении направления перемещения могут быть использованы простирания и других структур, которые являются следами движения плит. Например, асейсмичные вулканические хребты в океанах (такие, как Гавайско-Императорская цепь) считаются следами прохождения литосферных плит над горячими точками в мантии Земли. Следовательно, по простираниям таких хребтов можно рассчитать положение полюса вращения литосферной плиты по отношению к горячей точке или к мантии Земли.
Ориентировка напряжений в очагах землетрясений является одним из надежных и бесспорных указаний на направление относительного перемещения плит, взаимодействием которых обусловлены данные землетрясения.
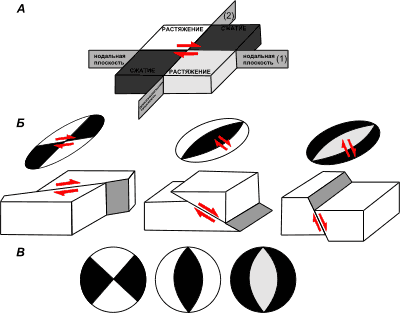
Рис. 15. схема решения фокальных механизмов землетрясений. (c изменениями /avspir/)
А – принципиальная схема дислокаций в очаге землетрясения. Стрелки показывают направление движения в очаге. Надписи в квадратах отмечают характер регистраций волн на сейсмостанциях; Б – стереографические проекции типовых решений фокальных механизмов: а – для сдвига, б – для надвига (взброса), в – для сброса; В – типовые примеры смещений в очагах землетрясений: а – сдвиг, б – надвиг, в – сброс
Землетрясения, как установили сейсмологи, возникают в результате скалывания по трещинам, являясь следствием упругой деформации пород Наиболее распространенная кинематическая модель очага землетрясения исходит из представления о смещениях по paзрыву в результате действия пары сил (рис.15). При разрыве в окружающей среде распространяются во все стороны сейсмические волны как продольные, так и поперечные. Первые вступления этих волн на сейсмограммах обычно принадлежат продольным волнам. На сейсмостанции, находящиеся на разных расстояниях от эпицентра, первые вступления продольных волн приходят с разным знаком, будучи направленными либо к очагу землетрясения, либо от него Это отражает ориентировку напряжений в очагах землетрясений. При возникновении разрыва от очага землетрясения пойдут в разные стороны волны сжатия и волны растяжения. Непосредственно в самом очаге(см.рис.15) растяжение ориентировано по направлению простирания волн сжатия, а сжатие, напротив, по направлению волн растяжения.
Всего будет четыре области: две сжатия и две растяжения, расположенные симметрично относительно друг друга. Они разделены плоскостью (1), по которой происходит разрыв, и перпендикулярной ей вспомогательной плоскостью (2). Эти плоскости называются нодальными. По регистрации первых вступлений на сейсмостанциях можно оконтурить только сами четыре области или четыре квадранта, парно соответствующих сжатию и растяжению, и, следовательно, определить положение в пространстве нодальных плоскостей, но невозможно установить, какая из нодальных плоскостей является плоскостью смещения, а какая – вспомогательной. Выбор главной плоскости смещения производится главным образом по геологическим материалам, исходя из приуроченности землетрясения к разрывам того или иного простирания.
Обычно решения фокальных механизмов землетрясений даются в виде азимутов простираний и углов падений нодальных плоскостей, а также ориентировки осей сжатия и растяжения, располагающихся под углами 45° к нодальным плоскостям. для определения относительного перемещения плит используется горизонтальная проекция вектора смещения, выражаемого в азимутах простирания векторов смещения. Азимуты векторов смещения всегда перпендикулярны вспомогательной плоскости. Именно их направления являются выдержанными вдоль простирания границы плит.
Решения фокальных механизмов принято изображать графически в виде стереографической проекции нодальных плоскостей на нижнюю полусферу с центром в очаге землетрясения. Типичные решения для механизмов сдвига, сжатия и растяжения приведены на рис.15. Квадранты сжатия показаны темным, квадранты растяжения – белым.
Измерение скоростей относительного движения плит
Скорости перемещения плит достаточно надежно устанавливаются в срединно-океанских хребтах по расстояниям между идентифицированными магнитными аномалиями. В океанах задача сводится к установлению скорости спрединга. Расстояние между одновозрастными магнитными аномалиями, расположенными по разные стороны от оси или между какой-либо аномалией и осью спрединга отвечает величине соответственно полного или половинного спрединга (если он симметричный), которая раскроется за данный промежуток времени. Расстояние между смежными аномалиями, расположенными по одну сторону от оси спрединга, отвечает величине полуспрединга за прошлый отрезок времени, определяемый возрастом этих магнитных аномалий. Чем меньше временной интервал, для которого измеряются величины раскрытия, тем полученные скорости будут ближе к мгновенным скоростям.
Скорость движения плит вдоль внутриконтинентальных рифтовых зон может быть выявлена, исходя из величины раскрытия грабенов. молодые смещения по многим сдвигам оцениваются по расстояниям между разобщенными одинаковыми формами рельефа или структурными элементами (например, речными долинами, моренными грядами, лавовыми потоками, массивами интрузивных пород).
При составлении задач использовались следующие условные обозначения:
Р – полюс вращения
φ – широта полюса вращения: с.ш. – "+" ю.ш. – "−"
λ – долгота полюса вращения: в.д.– "+" з.д.– "−"
ω – угловая скорость, угол поворота град/млн лет, вращение против часовой стрелки (левостороннее) – "+", по часовой стрелке (правостороннее) – "−"
А/В – перемещение плиты А относительно плиты В (Hапример, СА/ЮА перемещение Североамериканской плиты относительно Южноамериканской)
D – склонение палеомагнитного полюса
J – наклонение палеомагнитного полюса
Φ – широта палеомагнитиого полюса
Λ – долгота палеомагнитного полюса
v – линейная скорость
Дуги больших и малых кругов
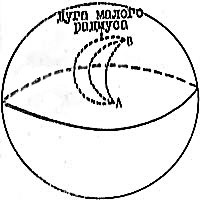
Рис. 16. Дуги большого (АВ) и малого (пунктир) круга.
Линии на сфере являются дугами, имеющими определенный радиус. Различаются дуги больших и малых кругов (рис. 16). Радиус дуги большого круга равен радиусу сферы.
Через две точки (А и В) можно провести лишь одну дугу большого круга. Она отвечает кратчайшему расстоянию между точками А и В. Расстояние, т.е. величина дуги, может измеряться в линейных величинах (км, м, см), и в угловых – градусах. Например, Расстояние от Москвы до Ленинграда равное 650 км, составляет в градусах 5,86° дуги большого круга (1° = 111 км). Дуги малых кругов имеют радиус, меньший радиуса сферы. их можно провести неограниченное количество через две точки. Например, на глобусе меридиан является дугой большого круга, а широты – дугами малых кругов. Это в равной степени относится к Эйлеровым меридианам и широтам. Трансформные разломы, которые отвечают Эйлеровым широтам, следуют концентрически расположенным дугам малых кругов.
Сферические треугольники
Большинство задач тектоники плит связано с решением сферических треугольников, стороны которых ограничены отрезками дуг большого круга.
а. Определение на сфере расстояния между двумя точками (определение величины дуги).
Даны две точки с координатами: 1 точка – широта X1, долгота Y1, 2 точка – широта X2, долгота Y2. Расстояние между этими точками по дуге большого круга – Д – будет равно:
Д = arccos((sinX1*sinX2) + (cosX1*cosX2)*cos(Y2-Y1))
б. Решение прямоугольного сферического треугольника (рис.17,a).
Даны А,В,С – углы треугольника, град, С =90°, a,b,c – противостоящие углам стороны дуг большого круга, град.
sina = sinC*sinA; tga = tgс*cosB; sinb = sinC*sinB tgB = tgc*cosA; tga = sinb*tgA; cosB = cosb*sinА; tgb = sina*tgB; cosА = cosa*sinB; cosc = cosa*cosB; cosC = ctgA*ctgB
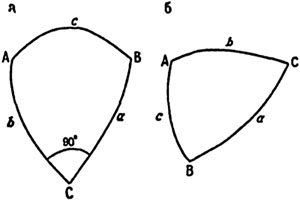
Рис. 17. Сферические треугольники: а – прямоугольный, б – косоугольный
в. Решение косоугольников треугольника
Даны А,В,С – углы треугольника, град, a,b,c – противостоящие углам стороны дуг большого круга, град.
| 1. | sina | = | sinb | = | sinc | – теорема синусов |
| sinA | sinB | sinC |
2. cosa = cosb*cosc + sinb*sinc*cosA
3. cosA = -cosB*cosC + sinB*sinC*cosA
4. sina*ctgb = ctgB*sinC + cosa*cosC
5. sinA*ctgB = ctgb*sinC - cosA*cosC
Порядок вычислений:
| Исходные данные | Формулы расчета искомых параметров (в скобках – номера формул) |
| а,в,с | А (2), Б и С (1) |
| А,В,С | а (3), в и с (1) |
| а,в,С | B(4), A и с (I) |
| А,В,с | в (5), а и С (I) |
| а,в,В | А (I), с (5), С (1) |
| А,В,в | а (1), С(4), с (I) |
г. Расчеты линейной и угловой скоростей.
Зная расстояние в градусах дуги большого круга (Д) заданной точки от полюса вращения плит, вычислить угловую скорость W, град/млн лет по линейной скорости v , см/год в этой же точке, и наоборот, вычислить линейную скорость точки по известной угловой скорости
| W = | v*106 | , (1) |
| R*sinD*0.1745*105 |
где R – радиус Земли, равный 6.37*108 см.
| W = | v | , (2) |
| 11.12*sinD |
v = W*11.12*sinD (3)
Задача 1. Составить программу определения величины отрезка дуги большого круга между точками А и В с координатами X1, Y1 для точки А и X2, Y2 для точки В.
Задача 2. По составленной программе определить расстояние между точками с координатами:
а) 30 ю.ш., 15 в.д. и 30 с.ш., 45 в.д.;
б) 20 с.ш., 160 в.д. и 15 ю.ш., 150 з.д.;
в) 40 с.ш., 130 в.д. и 10 ю.ш., 20 з.д.
Ответ: а) 66,45; б) 60,34; в) 139,9
Задача 3. Составить программу расчета угловой скорости по линейной скорости v, если известны координаты точки (в которой замерена линейная скорость) X1,Y1 и координаты Эйлерова полюса X2, Y2. Составить подобную программу расчета линейной скорости, если известна угловая скорость.
Решение:
1. Input X1, Y1, X2 Y2, V
2. D = arccos(sinX1*sinX2)+(cos X1-cos X2)cos(Y2-Y1)
3. W=V/11,12 sin D
4. print W
5 end
Задача 4. Составить программу решения сферических треугольников при заданных параметрах: А, В,С – углы треугольника, град; а,в,с – противостоящие стороны треугольника дуги большого круга, град.
Задача 5. Эйлеров полюс раздвижения Евразиатской и Североамериканской плит находится в точке Р (65 с.ш., I32 в.д.), угловая скорость равна 0,25 град/млн лет. Определить линейные скорости в точках: а) 90, О (Северный полюс); б) 40 с.ш. 30 в.д. (Азорские острова).
Ответ: а) 1,17 см/год; б) 2,67 см/год.
Задача 6. Эйлеров полюс движения Индийской плиты относительно Евразиатской находится в точке Р (19,7 с.ш., 38,5 в.д.), угловая скорость равна 0,7 град/млн лет. Определить линейную скорость в точке 30 с.ш., 81 в.д. (Гималаи).
Ответ: 4,97 см/год.
Движение литосферных плит на сфере. Расчет направления движения плит
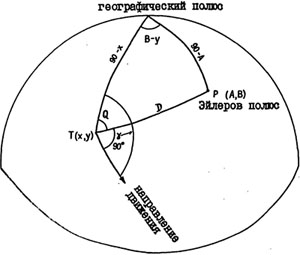
Рис. 18. Вычисление азимута движения плиты
Вторым после скорости параметром перемещения плит является направление движения. Оно дается в виде азимута, который представляет собой правый угол, образованный направлением движения плит с меридианом. Если известны координаты Эйлерова полюса, то вычислить азимут движения можно, используя решения сферических треугольников. Даны координаты Эйлерова полюса Р (А, В), координаты точки Т (Х,У). Надо найти азимут движения (рис. 18).
Решение:
1. γ = 90 + Q
2. Находим расстояние Д между Т и Р
3. Находим cosQ по формуле (2) из решений косоугольных сферических треугольников
cosQ = (cos(90-A) - cos(90-X)cosD)/(sin(90-X)*sinD) = (sinA-sinX*cosD)/(cosX*sinD)
Q = arccosQ
Задача 7. Составить программу расчета азимута движения плит, если известны координаты Эйлерова полюса и данной точки. Учесть в программе различные варианты взаимного расположения точек и нахождения в разных полушариях Земли.
Задача 8. Найти азимут движения плиты I относительно плиты II в точке Т (10 с.ш., 10 в.д.), если координаты Эйлерова полюса Р (55 с.ш., 30 з.д.)
Ответ: γ= 105,4.
Расчет параметров вращения плит. Самой распространенной задачей тектоники плит является использование первичных данных для расчета параметров движения плит: определения координат полюса и угловой скорости вращения.
Расчет угловой скорости, если известна линейная скорость в какой-либо точке, выполняется по формуле (2), см. выше. Для вычисления координат Эйлерова полюса используется то его свойство, что он лежит на пересечении перпендикуляров, проведенных к азимутам направления плит по меньшей мере в двух точках.
Алгоритм расчета координат Эйлерова полюса, если известны азимуты направлений движения плиты в двух точках, приводится ниже.
Вычисление Эйлерова Полюса по азимутам (рис. 19).
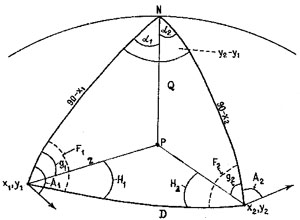
Рис. 19. Вычисление координат Эйлерова полюса по азимутам
Даны координаты точки 1: X1, Y1, азимут движения A1, точки 2 X2, Y2, азимут A2
Найти координаты Эйлерова полюса
Широта Эйлерова полюса φ = 90°- Q
Долгота Эйлерова полюса λ = Y1 + α1
находим D (Напомним, угол между направлением на полюс вращения и направлением движения равен 90°.)
G1 = A1 - 90
G2 = 90 - A2
находим F1 и F2 (используя теорему синусов)
| sin(90 - X2) | = | sin D |
| sin F1 | sin (Y2-Y1) |
| F1 = arcsin | sin(90 - X2) * sin(Y2-Y1) |
| sin D | |
| F2 = arcsin | sin(90 - Xl) * sin(Y2-Y1) |
| sin D | |
| H1 = F1 - G1 | H2 = F2 - G2 |
находим Z (используя формулу (5))
(sinH1/tgH2) = (sinD/tgZ) - cosH1*cosD
(sinD/tgZ) = (sinH1/tgH2) + cosH1*cosD
Z = arctg(sinD/(sinH1/tgH2)+cosH1*cosD)
6. находим α1 (используя формулу (4))
sin(90-X1)/tgZ = (sinG1/tgα1) + cos(90-X1)*cosG1
(sinG1/tgα1) = sin(90-X1)/tgZ - cos(90-X1)*cosG1
α1 = arctg(sinG1/(sin(90-X1)/tgZ) - cos(90-X1)*cosG1)
6. находим Q (используя теорему синусов)
(sinZ/sinα1) = (sinQ/sinG1)
Q = arcsin(sinZsinG1/sinα1)
Обычно для расчета координат Эйлерова полюса используются не две, а значительно большее количество точек (до 100). На рис.20 видно, что когда мы имеем больше двух точек, перпендикуляры к азимутам из-за погрешностей в замерах или по другим причинам образуют целое облако пересечений. В этом случае координаты полюса должны рассчитываться статистически с определением точки, наилучшим образом отвечающей конкретным данным. Облако рассеивания рисует по существу доверительный эллипс, размеры которого определяют степень достоверности расчетов. Для вычисления статистического полюса используются достаточно сложные программы, пакеты которых имеются в вычислительных центрах.
Задача 9. Составить программу и рассчитать координаты полюса вращения, если известны азимут движения плиты в точке A1 с координатами X1, X2, и азимут движения в точке A2 с координатами:
a) X1=50°с.ш., Y1= 40°в.д., Аз = 120°; б) X2= 30°с.ш., Y2=140°в.д., Аз = 68°.
Ответ: φ =69.63°с.ш., λ = 83°в.д.
Относительные движения литосферных плит

Рис. 20. Облако рассеивания (доверительный эллипс)
При анализе движения и взаимодействия плит постоянно необходимо знать, что является системой отсчета, по отношению к чему устанавливается движение плит. Например, когда говорится, что Североамериканская плита движется в Северной Атлантике на запад, то надо знать, по отношению к какой плите. В данном случае по отношению к Евразиатской или Африканской. Но, скажем, по отношению к Тихоокеанской плите Североамериканская плита движется на юго-восток. Евразиатская плита движется по отношению к Северной Америке на восток, а между собой они сближаются, перемещаясь в широтном направлении. Поэтому каждый раз, когда заходит речь о движении и взаимодействии плит, необходимо определить по отношению к чему идет отсчет движения. В противном случае можно получить ложные результаты.
Задача 10. В Северной Атлантике вдоль оси спрединга Евразиатская плита отодвигается от Североамериканской по азимуту 94° со скоростью 2,5 см/год. Определить векторы и скорость движения: a) Североамериканской плиты относительно оси спрединга; б) Североамериканской плиты относительно Евразиатской; в) Евразиатской плиты относительно оси спрединга; г) оси спрединга относительно Евразиатской плиты; д) оси спрединга относительно Североамериканской плиты.
Вращение плит
Для реконструкций былого расположения литосферных плит, понимания современного взаимодействия и оценки взаимодействия в будущем необходимо перемещать их по сфере, т.е. осуществлять вращение. Для этого должны быть известны параметры вращения: координаты Эйлерова полюса и угол поворота. Без такого рода вращения не обходится почти ни одно плитно-тектоническое исследование. Обычно в памяти ЭВМ содержатся оцифрованные контуры материков, линейных магнитных аномалий, трансформных разломов и других структурных элементов. При введении параметров вращения и соответствующих командах весь массив данных вращается и, если есть вывод на графопостроитель, то все контуры рисуются в новом положении. Сейчас все большее распространение получили графические дисплеи, на которых можно "на глаз" вращать плиты, добиваясь их наилучшего взаимного расположения, и лишь после этого выводить полученную карту на графопостроитель.
В основе всех преобразований лежит схема, изображенная на рис.19. Задача сводится к тому, что если известны координаты точки Т, то надо найти координаты повернутой точки T1. Алгоритм решения этой задачи приводится ниже (рис. 21).
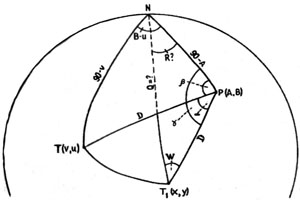
Рис. 21. Определение координат повернутой точки
Даны: 1) координаты Эйлерова полюса Р: широта А и долгота В; 2) угол поворота α ; 3) координаты точки Т: широта V и долгота U. Например, А = 50°с.ш., В = 60°в.д., α = 30°, V = 10°с.ш., U = 20°в.д.
Найти: 1) координаты повернутой точки Т1; 2) широту X; 3) долготу Y.
Решение:
1. X = 90 − Q ; Y = B − R
2. находим D, расстояние между Р и Т => (51,833°)
3. находим γ = β + α
β = arcsin(sin(90-V)*sin(B-U)/sinD) => (53,625°)
Если (90-V)>D и ???>(90-А), то β = 180 − β
(126.375°) (γ = I56°376)
4. находим W, (используя формулу (4) из решений сферических треугольников)
W = arctg(sinγ/(sinD/tg(90-α))-cosD*cosγ)
5. находим Q и X
Q = arcsin(sin(90-α)sinγ/sinW)
Q = 89,53°; X = 0,47° с.ш.
6. находим R и J
R = arcsin(sinD*sinW/sin(90-α))
R = 18,36°; J = 41,634°в.д.
Задача 11. Составить программу и рассчитать координаты точки T1, если известны координаты Эйлерова полюса Р (А,В), координаты точки Т0 и угол поворота α (программа вращения). Учесть при составлении программ направление вращения (по или против часовой стрелки), варианты положения точки T0 относительно полюса вращения и относительно земных полушарий.
Задача 12. Координаты Эйлерова полюса Р (50°с.ш., 60°в.д.), координаты точки T0 (Ю°с.ш., 20°в.д.), угол поворота = 30° (против часовой стрелки). Определить координаты точки T1.
Ответ: 0,59°с.ш., 41,63° в.д.
Задача 13. Дан полюс вращения Евразиатской и Аравийской плит в точке Р (30,0), угловая скорость сближения плит ω = 0,36 град/млн лет. Каковым будет взаимодействие плит: а) в районе Кавказа в точке А (42,45), если граница плит простирается СЗ 290 ? б) в районе хребта Загрос в точке В (33,50), если граница плит простирается здесь СЗ 330 ?
Ответ: а) Аз 356°, скорость 2,45 см/год; 6) Аз 10°, скорость 2,7 см/год.
Задача 14. Полюс вращения Тихоокеанской плиты относительно Камчатки находится в точке Р (50°с.ш., -75°з.д.), скорость сближения плит ω = 0,852 град/млн лет. Каковым будет взаимодействие плит: а) в Камчатском желобе, в точке А (52, 160), если
желоб простирается СВ 40°; б) 13 районе Командорских островов в точке В (55, 167), если граница плит простирается здесь СЗ 310?
Ответ: а)Аз.304°, скорость 0,8 см/год; б) Аз. 310°, скорость 8,4 см/год
Мгновенные, конечные и дифференциальные движения литосферных плит
Мгновенные движения – это те перемещения, которые регистрируются за крайне короткий в геологическом смысле промежуток времени. Речь, как правило, идет об отрезке времени меньшем 1 млн лет, и даже еще меньшем, т.е. о современных движениях. В этом случае вектор дается только в виде скорости и в виде азимута прямой, касательной к дуге направления движения. Современные мгновенные движения проявляются в виде землетрясений, при этом параметры движения получаются в результате решения механизма очагов землетрясений.

Рис. 22. Конечное (А0A1) и дифференциальные (А0q1, q1q2, q2q3, q3A1) движения
Конечное движение представляет собой перемещение плиты за какой-либо промежуток времени. Например, за время Т точка А0 перешла в положение A1 (рис. 22). Перемещение выражается в виде отрезка дуги малого круга, а его величина – углом поворота из Эйлерова полюса.
Конечное перемещение может быть суммой малых перемещений (см.рис.22), когда точка А0 занимает последовательные положения q1, q2, q3 и, наконец A1
Каждый из отрезков отвечает своей дуге малого круга, причем ориентировка этих отрезков может совершенно пнипидмть с направлением конечного перемещения. Такие движения, составляющие какое-либо конечное перемещение, называются дифференциальными (или стадийными). (Дифференциальные движения, в свою очередь, являются конечными по отношению к более дробным перемещениям.)
Очень часто в практике исследований нам известны конечные перемещения в течение каких-то двух интервалов геологического времени, например, с 80 млн лет до современности и с 50 млн лет до современности. Чтобы представить, какие события разворачивались с 80 до 50 млн лет, надо знать параметры дифференциальных движений двух плит за этот промежуток времени. Следовательно, стоит задача расчета дифференциальных движений.
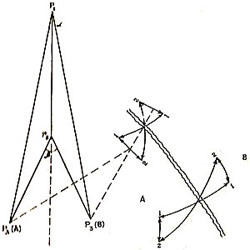
Рис. 23. Определение полюсов дифференциальных движений плит.
Решение этой задачи осложнено тем, что мы должны выбрать систему отсчета: по отношению к какой плите – А или В – мы будем рассчитывать параметры дифференциальных движений. Можно рассчитать два варианта решения, когда плита А принимается условно неподвижной (фиксированной) или же когда плита В принимается условно неподвижной и взята за систему отсчета.
Графически варианты решений продемонстрированы на рис. 23, граница плит А и В показана разрывом, конечное движение между точками I-I отвечает полюсу Р1 а между точками 2-2 – полюсу Р2. Следует найти полюс дифференциального движения Р3, отвечающий движению точки I к точке 2.
Из рисунка видно, что будет два положения полюса Р3, одно из которых привязано к плите А – Р3(А), а другое – к плите В – Р3(В). В расчетных таблицах дифференциальных движений всегда указывается, по отношению к какой плите приводятся параметры движения двух плит. Схема расчета приведена ниже при рассмотрении задачи тройного сочленения плит.
Метод конечного совмещения
Для определения параметров движения плит и палинспастических реконструкций широко используется метод наилучшего совмещения контуров. Именно этот метод использовал А.Вегенер, когда впервые пытался "закрыть" Атлантический океан, добиваясь наилучшего совмещения береговых линий Африки и Америки. До сих пор очертания берегов, контуры шельфа, континентального подножья или отдельные изобаты принимаются в качестве объектов для совмещения, расположенные по разные стороны от срединно-океанских хребтов. Применяется также совмещение отдельных разломов, подводных гор, складчатых сооружений и других структур, которые по предположению были разорваны и отодвинуты по разные стороны океана.
Наиболее убедительно этот метод используется применительно к линейным магнитным аномалиям океанов, которые, как известно, связаны с инверсиями магнитного поля Земли. Идентифицированные магнитные аномалии показывают возраст океанского ложа в данном месте. Каждая магнитная аномалия возникла в зоне оси спрединга, где была разорвана на две части, оказавшиеся впоследствии симметрично расположенными на некотором удалении от оси спрединга.
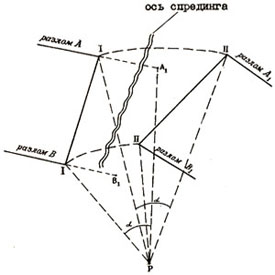
Рис. 24. Определение конечных параметров перемещения плит методом конечного совмещения
Совмещая одновозрастные аномалии, находящиеся по разные стороны от оси спрединга, мы получаем реконструкции океана (и смежных континентов) на отдельные моменты геологического времени. Это самый распространенный способ составления палинспастических реконструкций на поздний мезозой и кайнозой, т.е. на тот промежуток времени, для которого известны магнитные аномалии в океанах.
На рис. 24 показан принцип такого совмещения. При этом, конечно необходимо знать хотя бы одну пару точек, которые судя по имеющимся данным, были совмещены ранее. В случае магнитных аномалий такими точками являются места их пересечения трансформными разломами. Дальнейшая процедура несложна. Чтобы отыскать полюс вращения следует соединить два совмещаемых контура дуг большого круга, восстановить к их середине перпендикуляры, и пересечение даст точку полюса (Р). Угол α будет отвечать величине поворота
В реальности дело обстоит значительно сложнее, так как необходимо учитывать совмещение длинных изломанных или искривленных (береговые очертания) линий, которые идеально никогда не совмещаются. Поэтому полюс вращения отыскивается статистически с определенной погрешностью, величина которой определяется доверительным интервалом. Работа на графическом дисплее позволяет добиваться наилучшего совмещения визуально.
Расчет параметров движения литосферных плит в точке тройного сочленения
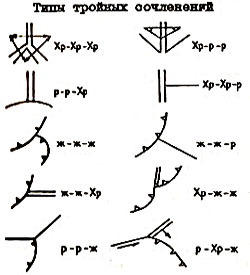
Рис. 25. Типы тройных сочленений литосферных плит
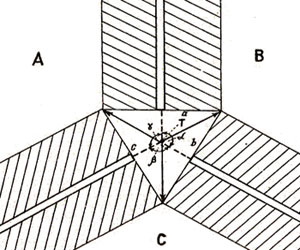
Рис. 26. Расчет скоростей наращивания литосферных плит в случае тройного сочленения Хр-Хр-Хр в точке Т. Заштрихованные участки – участки новой коры. С течением времени каждая ось будет наращиваться на отрезки Тa, Тb, Тc соответственно
Точка, где соприкасаются границы трех плит, получила название точки тройного сочленения. В ней могут сходиться границы трех типов: наращивания, скольжения, поглощения в любых сочетаниях. Если обозначить границы наращивания (срединные хребты) – Хр, границы поглощения (желоба) – Ж, границы скольжения (трансформные разломы) – Р, тогда типы тройного сочленения будут выглядеть как соединения символов, например, Хр-Ж-Р или Хр-Хр-Хр. Всего возможно 10 вариантов сочетаний границ плит (рис. 25). Из них наиболее распространенные; Хр-Хр-Хр (например, Галапагосская точка, точка Буве и др.); Хр-Хр-Р (например, Азорская); Хр-Р-Р (например, Южно-Байкальская точка) и др. Сочленение типа Ж-Ж-Ж встречается в юго-восточной части о.Хонсю (Япония). Типы тройных сочленений Хр-Хр-Хр, Хр-Хр-Р, Хр-Р-Р – устойчивы, другие, например, Хр-Хр-Ж или Хр-Р-Ж неустойчивы и быстро меняют свою конфигурацию.
Взаимное перемещение границ плит и точек тройного сочленения видно на примере сплетения типа Хр-Хр-Хр (рис. 26). Если принять точку тройного сочленения Т за неподвижную, то относительно нее литосферные плиты А,В и С переместятся на величину, обозначенную на рисунке толстыми стрелками. Одновременно должны наращиваться оси спрединга, т.е. и сами хребты должны смещаться по простиранию в сторону от точки тройного сочленения. Скорость наращивания осей спрединга (пунктирные линии на рис.26) может быть рассчитана по формуле
| Tb = | b + a*cosα |
| 2sinα |
где Tb – скорость наращивания, ac и bc – скорости спрединга в смежных осях, β – угол между ними. Например, если скорости спрединга равны: а = 3,2 см/год, b = 3,8 см/год, а c = 3,5 см/год, α = 120°, β = 132° и γ = 108°, то скорость наращивания границ для оси А/В будет 1,87 см/год, В/С – 0,64 см/год и для А/С – 1,06 см/год. Из этой простой геометрии следует, что оси спрединга продвигаются по направлению к точке тройного сочленения. Действительно, следы такого продвижения обнаруживаются в ряде срединных хребтов, например, в Галапагосской оси спрединга. Из постулата жесткости литосферных плит вытекает, что если плиты движутся, то движение трех плит, сходящихся в одной точке сочленения, должны быть строго увязаны между собой. Например, если мы имеем три плиты А,В,С, сходящиеся в одной точке, то в случае, когда одна плита условно неподвижна (плита А) (см.рис.26), плиты В и С будут смещаться относительно плиты А. Допустим, что каждая из них будет отодвигаться от плиты А. Тогда между плитами В и С неизбежно появится зияние. При этом величина относительного перемещения плит В и С зависит от величины и направления их перемещения относительно плиты А. Математически геометрическая сумма векторов относительного движения литосферных плит должна быть равной нулю.
AVB+ВVC+АVС = 0 или А/В + В/С + А/С = 0.
Скорость движения плиты А относительно плиты В равна скорости движения плиты В относительно А, но противоположна ей по знаку.
Если мы располагаем данными конкретных наблюдений по направлениям и величинам относительного перемещения литосферных плит, то их геометрическая сумма должна быть равной 0. В случае, если равенство отсутствует, надо искать причину невязки.
Довольно часто мы имеем данные о векторах движения каких-то двух плит относительно третьей, а вектор движения этих двух плит относительно друг друга неизвестен. Для нахождения параметров движения относительного перемещения двух плит необходимо решить задачу тройного сочленения. Пусть у нас имеются данные о векторах С/А и В/А и нужно найти В/С. Тогда В/С = В/А+С/А. Следует обратить внимание на порядок записи. Он помогает не запутаться в определении искомого вектора. Во второй части равенства в числителях ставятся символы плит, относительные параметры движения между которыми известны, а в знаменателе – символ плиты, по отношению к которой эти движения неизвестны (может быть, конечно, и другой условный характер записи).
Поскольку все три вектора скоростей, рассматриваемых в задаче тройного сочленения, лежат в одной плоскости, то полюса вращения должны располагаться на одной дуге большого круга, а искомый полюс – в той точке, где линейные скорости, отвечающие угловым скоростям из двух неизвестных полюсов вращения, направлены в одну сторону и равны друг другу (см. ниже).
Используя серию точек тройного сочленения и последовательно проводя замыкание движений вокруг них, можно провести глобальную увязку относительных движений всех литоеферных плит на земной сфере. Сумма этих движений должна быть равна нулю, т.е. количество общего наращивания литосферы должно быть равно количеству поглощения.
Решение задач тройного сочленения необходимо, во-первых, для того, чтобы по движениям двух пар плит дать заключение о взаимодействии третьей пары плит, во-вторых, чтобы можно было провести замыкание движения плит в региональном и глобальном масштабах, в-третьих, чтобы получить параметры дифференциальных движений из конечных или, наоборот, по сумме дифференциальных движений рассчитать параметры конечных перемещений.
В повседневной практике постоянно приходится решать векторные диаграммы. Суть задач сводится к тому, что в какой-то заданной или интересующей нас точке известны два вектора движений и надо определнить третий. Чтобы не запутаться в сложении векторов, следует помнить об упомянутом выше правиле выбора системы отсчета и порядке записи. Построение векторшп диаграмм дает возможность определить какие движения и какие тектонические условия следует ожидать в каждом конкретном расчете.
Решение задач тройного сочленения на ЭВМ сводитоя к тому, что по известным параметрам вращения двух пар плит находятся параметры вращения третьей пары плит. При этом в качестве основы используются приведенные выше формулы.
Следует указать, что должен быть разный подход к решению задач тройного сочленения в системе мгновенных движений и при наличии параметров дифференциальных и конечных вращений.
Задача 15. Нарисовать типы тройного сочленения литосферных плит. Найти и показать на карте наиболее яркие примеры.
Задача 16. В районе Азорских островов в точке с координатами 37°с.ш., 30°з.д. сочленяются, границы Евразиатской (ЕА), Североамериканской (СА) и Африканской (АФ) плит. Вектор ЕА/СА равен 97°, скорость 2,5 см/год. Вектор АФ/СА = Аз 102°, скорость 2,3 см/год. Найти лектор АФ/ЕА. Какие структуры можно ожидать в данном месте?
Задача 17. Какие структуры можно ожидать в точке В с координатами 37°с.ш., 20°з.д., если вектор ЕА/СА = Аз 101°, скорость 2,5 см/год, и вектор АФ/СА = Аз 101°, скорость 2,2 см/год. Найти вектор АФ/ЕА и скорость АФ/ЕА.
Задача 18. В районе Кавказа в точке С с координатами 40°с.ш., 40°з.д., вектор ЕА/СА = Аз 120°, скорость 2,1 см/год, вектор АФ/СА 97°, скорость 1,9 см/год. Найти вектор АФ/ЕА, скорость АФ/ЕА. Какие структуры стоит ожидать в этом месте?
Задача 19. районе Памира в точке с координатами 40°с.ш., 75°в.д. взаимодействуют Индийская (Ин) и Евразиатская (ЕА) плиты. Какие геодинамические условия господствуют в этой точке и какие структуры следует ожидать, если вектор ЕА/АФ = Аз 204°, скорость 1,1 см/год; вектор Ин/АФ = Аз 326°, скорость 4,0 см/год?
Задача 20. Вблизи Галапагосских островов в Тихом океане в точке с координатами 2°с.ш., 102°з.д. сочленяются границы трех плит – Кокос (Ко), Наска (На) и Тихоокеанской (Ти). Вектор Ко/Ти = Аз 83°, скорость 15,0 см/год, вектор На/Ти = Аз 99°, скорость 14,0 см/год. Найти вектор Ко/На и скорость Ко/На.
Задача 21. Хребет, разделяющий плиты А и В, вытянут строго меридионально (Аз =0°), скорость VB/A = 60 мм/год. Хребет, разделяющий плиты В и С, имеет Аз = 120°. Хребет, разделяющий плиты А и С, имеет Аз = 270°. Определить азимуты и величины относительных скоростей VС/В, VА/С. Построить векторные диаграммы.
Ответ: VС/В = 120 мм/год, Аз C/B = 210°; VА/С = 104 мм/год, AзС/А 0°
Задача 22. Тройное сочленение (Ж-Ж-Р), плиты А,В и С. Правосторонний трансформный разлом (Аз = 45°) мигрирует вдоль желоба,имеющего меридиональное простирание (Аз = 0°). Предположим, что АзВ/А = 270° VВ/А = 50 мм/год, VВ/С = 50 мм/год. Определить: 1) AзС/А, VС/А; 2) азимут и скорость миграции трансформного разлома вдоль желоба.
Ответ: 1)Аз С/А = 250°, VС/А = 92,4 мм/год.
Задача 23. Тройное сочленение Ж-Ж-Р, плиты А,В,С. Азимут перемещения плиты А относительно В по трансформному разлому составляет АзА/В = 0° Азжел.АС = 220°, Aзжел.BC = 180°. Предположим, что АзС/В перемещения плиты С относительно плиты В равен АзС/В = 90°, скорость VС/В = 10 мм/год, VА/В = 50 мм/год. Определить АзА/С и VА/С.
Ответ: АзА/С = 191°, VА/С = 50 мм/год.
Задача 24. Тройное сочленение Ж-Ж-Х, плиты А,В и С. Хребет имеет Азхр = 135°, желоб имеет Азжел = 0°. Предположим, что AзВ/А- 270°, VB/A = 50 мм/год, VC/B = 40 мм/год. Определить AзС/А и VС/А, а также направление и скорость миграции хребта относительно плиты А.
Ответ: AзС/А = 250°, VС/А= 83 мм/год; Азхр/А = 180°, Vхр/А = 50 мм/год.
Расчет параметров движения литосферных плит в случае тройного сочленения
В системе мгновенных движений, как указывалось выше, векторы строго приложены к точкам и не имеют конечных размеров, т.е. точки находятся в центре векторных треугольников.

Рис. 27. Решение задач тройного сочленения плит. Определение координат и параметров движения плит В и С, если известны параметры движения и координаты Эйлерова полюса движения плиты А относительно В и плиты А относительно плиты С.
На рис. 23 показано тройное сочленение плит А,В,С. В точках I и II нанесены векторные диаграммы. Они помогают найти положение полюсов вращения в точке пересечения перпендикуляров к векторам. Полюс вращения плит А и В находится в точке P1, угловая скорость α; плит А и С – в точке P2, угловая скорость γ. Найти полюс вращения плит В и С, т.е. координаты точки P3 и угловую скорость β.
В расположении этих трех полюсов на сфере есть та закономерность, что они обязательно должны находиться на одной и той же дуге большого круга, а точка P3 будет находиться в том месте этой дуги, где линейные скорости, отвечающие угловым величинам α и γ будут равны. Это дает основу для решения задачи тройного сочленения. Если известно положение полюсов вращения двух пар плит РАВ и РАС, то положение полюса вращения третьей пары – РВС – будет находиться, как показано выше, в той точке, где линейные скорости двух других пар плит равны, т.е. выдерживается соотношение
αsin РАВ = γsin РАВ
где α и γ – угловые скорости вращения соответственно плит AВ и АС. (Это выражение получается по формуле определения линейной скорости в данной точке, если известна угловая скорость и расстояние до полюса вращения.) Отсюда расстояние от полюса РАВ до искомого полюса PВС будет определяться по формуле
| tg РАВРВС = | γsin РАВРВС |
| a+γcos РАВРAС |
а угловая скорость вращения плит В и С будет равна
| β = α | sin РBCРAС |
| sin РАВРAС |
Найдя дугу P2P3, мы, конечно, не получим сразу географические координаты. Они находятся следующим образом: 1) совместим один из полюсов, например, P1 с географическим Северным полюсом. Это делается вращением вокруг точки, расположенной на экваторе на расстоянии 90° от меридиана P1 на угол, равный разности 90° и широты P1; 2) вместе с P1 повернем точку P2; 3) определим в этой повернутой системе координат широту P3, равную 90° – P2P3. Ее долгота при этом будет отвечать долготе точки P2 в ее повернутом вместе с точкой P1 положении; 4) повернув теперь обратно точку P1 с географического полюса в исходное положение, а вместе с ней точку P3, получим истинное значение шроты и долготы полюса Р3.

рис. 28. Определение параметров дифференциальных движений плит
В системе конечных и дифференциальных движений к задаче тройного сочленения сведено рассмотрение движений одной пары плит, но за разные промежутки времени. Важно подчеркнуть, что здесь существуют два полюса, каждый из которых связан с одной из двух плит. Даны плиты А и В (рис. 28), граница между ними идет по двойной извилистой линии. На каждой плите показаны траектории конечного движения от точки 0 к точкам t1 и t2. Полюса находятся соответственно в точках P1 и P2. Углы вращения обеих плит одинаковы, но вращение направлено в противоположную сторону (в зависимости от того, какая влита выбрана за систему отсчета). Дифференциальные движения определяются отрезками t1 – t2. Они имеют разное расположение на плитах А и В в зависимости от системы отсчета. Соответственно будет два полюса дифференциального вращения, привязанные к плите А и В (точки Р(t1-t2)A и P(t2-t1)B). Положение полюсов Р3(А) и Р3(В) будет симметричным относительно дуги большого круга, соединяющего полюса P1 и P2. Искомые полюса будут находиться на угловых расстояниях от полюсов P1 и P2, соответственно на α и β, отвечающих углу поворота плит. Чтобы найти координаты полюсов Р3(А) и Р3(В) можно воспользоваться формулами расчета мгновенных полюсов. Величина P2P3 характеризующая широту, останется той же, а долгота в положении, когда точка P1 совмещена с географическим полюсом, будет отличаться от долготы точки Р2 на половину α соответственно с минусом для Р3(А) и с плюсом для Р3(В).
Задача 25. Составьте программу нахождения мгновенного полюса вращения плит В и С, если известны параметры вращения плит В/А и С/А.
Задача 26. Составьте программу нахождения дифференциальных полюсов плит для времени T2-T1, если известны полюса двух конечных вращений соответственно для времени T1 и T2.
Задача 27. Определить параметры конечных перемещений Южноамериканской плиты (ЮА) относительно Североамериканской плиты (СА) на время 180, 148, 127, 110, 79, 36 млн лет назад, которому соответствуют аномалии М29, М22, M11, М0, А34, AI3, если известны параметры конечного перемещения Северной Америки относительно Африки (АФ), Южной Америки относительно Африки на те же временные рубежи (см.таблицу).
| Магнитные аномалии, (время, млн лет) | Северная Америка / Африка | Южная Америка / Африка | ||||
| φ | λ | ω | φ | λ | ω | |
| A13(36) | 78 | 11.5 | 9.5 | 57.4 | -37.5 | 13.4 |
| А34(79) | 72.9 | -26.0 | 33.9 | 63.23 | -35.79 | 33.8 |
| М0(110) | 66.5 | -21.7 | 55.9 | 46.55 | -28.82 | 52.4 |
| M11(127) | 66.2 | -15.76 | 60.6 | 44.10 | -30.30 | 56.10 |
| M22(148) | 65.6 | -18.30 | 63.9 | 44.10 | -30.30 | 65.10 |
| Конечное совмещение (180) | 66.2 | -12.40 | 71.8 | 44.10 | -30.30 | 56.10 |
Ответ:
| ЮА/СА | φ | λ | ω |
| А13(36) | 19.06 | -56.11 | 6.43 |
| А34(79) | -18.12 | -71.86 | 6.08 |
| М0(110) | -35.50 | -72.70 | 19.40 |
| M11(127) | -32.10 | -83.40 | 24.14 |
| М22(148) | -39.50 | -87.60 | 24.16 |
| Конечное совмещение (180) | -45.0 | -102.20 | 30.85 |
Задача 28. Используя условия задачи 27, вычислить параметр дифференциального движения: 1) Южной Америки (ЮА) относительно Северной Америки; 2) Северной Америки относительно Южной Америки на указанные интервалы времени.
Ответ:
| Интервал времени | Относительно СА | Относительно ЮА | ||||
| Магнитные аномалии, время, млн лет | φ | λ | ω | φ | λ | ω |
| М22(180-148) | 55.61 | 24.10 | 8.79 | 38.72 | 31.00 | -8.79 |
| M22-M11(148-127) | 59.53 | -60.44 | 3.49 | 46.14 | -26.25 | -3.49 |
| M11-M0(127-110) | -20.73 | -117.8 | 5.95 | -10.32 | -109.8 | -5.95 |
| М0-А34(110-79) | -43.10 | -71.40 | 13.72 | -42.95 | -74.90 | -13.72 |
| А34-A13(79-36) | 70.40 | 14.45 | 4.32 | 64.80 | 16.80 | -4.32 |
| A13-0(36-0) | 19.96 | -56.11 | -6.43 | 19.06 | -56.11 | 6.43 |
Задача 29. Используя условия задачи 27, построить график относительного перемещения СА/АФ для произвольной точки, взятой на Североамериканской плите. Проделать ту же операцию для точки, взятой на Южноамериканской плите.
Задача 30. Используя результат решения задачи 27, построить график относительного перемещения ЮА/СА на указанные временные интервалы для произвольной точки на Североамериканской плите.
Задача 31. Используя результаты решения задачи 28, построить график перемещения Североамериканской плиты относительно Южноамериканской, и наоборот, Южноамериканской плиты относительно Северероамериканской для указанных временных рубежей. Сравнивать графики между собой, к также с графиком, полученным при решении задачи 30. При построении графиков брать одни и те же точки на СА и ЮА плитах.
Задача 32. Известны параметры конечных перемещений Южноамериканской плиты относительно Антарктиды (АН) (см. таблицу). Вычислить дифференциальные движения между ЮА/AН и АН/ЮА. Построить графики относительных перемещений этих литосферных плит для произвольно выбранных точек на ЮА и АН плитах.
Южной Америка/Антарктида
| Магнитные аномалии, время, млн лет | φ | λ | ω |
| A16(39) | -84.41 | -154.44 | -12.06 |
| A22(53) | -76.77 | -174.38 | -15.35 |
| A28(65) | -74.82 | -148.24 | -18.14 |
| А34(79) | -74.56 | -112.09 | -23.91 |
| M1(115) | -67.23 | -76.36 | -46.95 |
| Конечное совмещение | -57.87 | -89.85 | -45.87 |
Ответ:
| Интервал времени | Относительно Южной Америки | Относительно Антарктиды | ||||
| Магнитные аномалии, время, млн лет | φ | λ | ω | φ | λ | ω |
| M1(160-115) | 33.82 | -95.63 | -9.1 | 21.33 | -145.95 | 9.1 |
| М1-А34(115-79) | -59.35 | -52.22 | -24.34 | -54.42 | -69.23 | 24.34 |
| А34-A28(70-65) | -58.29 | -55.70 | -6.7 | -53.58 | -72.50 | 6.7 |
| A28-A22(65-53) | -50.88 | -97.31 | -3.39 | -47.58 | -110.88 | 3.39 |
| A22-A16(53-39) | -50.11 | -178.44 | -3.82 | -84.41 | -154.44 | 3.82 |
Задача 33. Даны координаты Эйлерова полюса вращения Евразиатской и Североамериканской плит (см. таблицу) на время 37, 48, 53, 83, 90 млн лет. Определить параметры дифференциальных движений Евразии относительно Северной Америки на этапы: 90-83; 83-53; 53-48; 48-37 млн лет.
Конечные вращения Евразиатской плиты относительно Североамериканской
| Время, млн лет назад | φ | λ | ω |
| 37 | 68.0 | 129.9 | -7.8 |
| 48 | 50.8 | 142.8 | -9.8 |
| 53 | 40.0 | 145.0 | -II.4 |
| 83 | 70.5 | I50.I | -20.3 |
| 90 | 75.5 | 152.9 | -24.2 |
Примечание. Координаты Эйлерова полюса вращения Североамериканской плиты относительно Евразиатской те же, но угол поворота будет иметь другой знак (ЕА/СА=-СА/ЕА).
Задача 34. Используя данные задачи 33, построить графики миграции Эйлеровых полюсов для конечных и дифференциальных движений ЕА/СА на указанные интервалы времени.
Задача 35. Даны координаты дифференциальных движений СА/ЕА и ЕА/СА. Определить параметры конечных движений СА/ЕА и ЕА/СА.
| Интервал времени | ЕА/СА | СА/ЕА | ||||
| Время, млн лет назад | φ | λ | ω | φ | λ | ω |
| 90-83 | 77.93 | -103.76 | 4.36 | 80.34 | -23.55 | -4.36 |
| 83-53 | 78.09 | -104.06 | 11.97 | 80.44 | -22.68 | -11.97 |
| 53-48 | -6.19 | 146.2I | 2.57 | -5.38 | 154.43 | -2.57 |
| 48-37 | 5.57 | 150.35 | 3.43 | 6.75 | 157.29 | -3.43 |
| 37-0 | 68.00 | 129.90 | 7.80 | 68.00 | 129.90 | -7.80 |
Задача 36. Используя данные задачи 35, определить угловые скорости вращения СА/ЕА на время 85, 60, 50, 30, 15 млн лет. Определить V=СА/ЕА на те же этапы для точки с координатами (30°-82°).
Ответ. Угловые скорости: 0,623; 0,399; 0,514; 0,211; 0,211 °/млн лет; линейные скорости в точке 30°-82°: 5,69 см/год, Аз 280°; 3,65 см/год, Аз 280°; 4,87 см/год, Аз 193°; 2,3 см/год, 258°;
Задача 37. Даны параметры относительных перемещений плит Земли на различные этапы. Используя глобальную увязку движения литосферных плит, определить параметры конечных движений каждой плиты плиты на этапы 37, 20, 10 млн лет; определить параметры дифференциальных движений этих плит на этапы 37-20, 20-10 млн лет.
| Плиты | Возраст | φ | λ | ω |
| АР/АФ | 20 | 36.50 | 18.00 | -6.10 |
| СМ/АР | 20 | 26.50 | 21.50 | 7.60 |
| МА/СМ | 100 | - | - | 0.00 |
| 123 | -13.10 | 319.00 | 8.10 | |
| 138 | -16.30 | 328.60 | 13.80 | |
| АН/АФ | 40 | 5.80 | 322.80 | 7.20 |
| 50 | 12.00 | 311.40 | 7.50 | |
| 83 | 19.70 | 316.20 | 19.20 | |
| 123 | -3.90 | 332.20 | 45.50 | |
| 138 | -2.40 | 327.30 | 55.40 | |
| АВ/АН | 37 | 11.90 | 34.40 | -20.50 |
| 42 | 10.30 | 34.80 | -23.60 | |
| 50 | 11.90 | 30.80 | -30.90 | |
| Ин/АВ | 50 | - | - | 0.00 |
| 63 | 8.90 | 333.40 | 17.20 | |
| 83 | 5.60 | 355.30 | 38.60 | |
| 123 | -9.60 | 9.70 | 59.10 | |
| 133 | II.10 | 3.50 | 62.10 | |
| ЮА/АФ | 40 | 59.00 | 325.00 | 14.90 |
| 50 | 63.00 | 324.00 | 20.10 | |
| 83 | 63.00 | 324.00 | 33.80 | |
| 138 | 44.00 | 329.40 | 57.00 | |
| АФ/СА | 37 | 70.50 | 341.30 | 10.40 |
| 66 | 80.80 | 351.40 | 22.50 | |
| 71 | 80.40 | 347.50 | 23.90 | |
| 75 | 78.30 | 341.40 | 27.10 | |
| 83 | 77.10 | 340.80 | 29.40 | |
| 119 | 66.30 | 340.10 | 54.30 | |
| 127 | 66.10 | 341.00 | 56.40 | |
| 145 | 66.10 | 341.60 | 59.80 | |
| 169 | 67.00 | 346.80 | 72.10 | |
| 180 | 67.00 | 348.00 | 75.60 | |
| Гр/СА | 37 | - | - | 0.00 |
| 48 | 13.00 | 302.00 | 1.10 | |
| 53 | 26.00 | 301.50 | 2.80 | |
| 83 | -69.60 | 46.60 | 9.50 | |
| 90 | -71.50 | 53.70 | 11.00 | |
| ЕВ/СА | 37 | 68.00 | 129.90 | -7.80 |
| 48 | 50.80 | 142.80 | -9.80 | |
| 53 | 40.00 | 145.00 | -11.40 | |
| 83 | 70.60, | 150.20 | -20.30 | |
| 90 | 75.50. | 153.00 | -24.20 |
Примечание. АФ – Африка, АР – Аравия, СМ – Сомали, АН – Антарктида, АВ – Австралия, Ин-Индия, СА – Северная Америка, ЮА – Южная Америка, Гр – Гренландия, ЕВ – Европа, МА – Мадагаскар.
Задача 38. Определить параметры конечных вращений литосферных плит по отношению друг к другу на указанные этапы, если известны параметры их конечных движений относительно горячих точек.
| Плита / горячая точка | Возраст | φ | λ | ω |
| Африка / горячая точка | 20 | -50.40 | 52.10 | 5.40 |
| 40 | -48.00 | 142.20 | 10.40 | |
| 60 | -44.20 | 131.40 | 14.60 | |
| 80 | -35.40 | 121.60 | 21.70 | |
| 100 | -29.00 | 133.40 | 27.90 | |
| 120 | -25.90 | 137.50 | 34.20 | |
| 140 | -23.70 | 134.00 | 34.00 | |
| 160 | -17.00 | 126.00 | 29.40 | |
| 180 | -5.50 | 112.90 | 23.80 | |
| 200 | 17.60 | 86.70 | 22.70 |
| Плита / горячая точка | Возраст | φ | λ | ω |
| Южная Америка / горячая точка | 20 | 21.60 | 3.02 | 5.73 |
| 40 | 78.96 | 2.36 | 5.10 | |
| 60 | 72.90 | 31.58 | 11.67 | |
| 80 | 59.72 | 51.49 | 17.74 | |
| 100 | 62.09 | 47.01 | 20.25 | |
| 120 | 58.63 | 33.41 | 22.30 | |
| 140 | 48.93 | 10.15 | 29.09 | |
| 160 | 46.03 | 7.74 | 35.99 | |
| 180 | 43.58 | 3.26 | 45.23 | |
| 200 | 40.73 | 1.12 | 58.75 |
| Плита / горячая точка | Возраст | φ | λ | ω |
| Северная Америка / горячая точка | 20 | 13.72 | 26.03 | 4.57 |
| 40 | 39.67 | 117.55 | 5.13 | |
| 60 | 48.28 | 104.59 | 12.34 | |
| 80 | 45.45 | 89.50 | 20.28 | |
| 100 | 54.75 | 82.93 | 28.30 | |
| 120 | 57.70 | 69.44 | 36.98 | |
| 140 | 57.27 | 59.84 | 42.24 | |
| 160 | 58.27 | 42.13 | 55.93 | |
| 180 | 58.31 | 27.44 | 71.33 | |
| 200 | 56.85 | 17.15 | 83.18 |
| Плита / горячая точка | Возраст | φ | λ | ω |
| Европа / горячая точка | 20 | -29.85 | 10.12 | 5.79 |
| 40 | -75.12 | 47.45 | 4.24 | |
| 60 | -12.42 | 39.50 | 5.88 | |
| 80 | -19.08 | 69.35 | 12.75 | |
| 100 | -3.71 | 73.01 | 15.24 | |
| 120 | 19.18 | 63.98 | 21.33 | |
| 140 | 24.85 | 57.51 | 26.66 | |
| 160 | 35.60 | 45.05 | 39.91 | |
| 180 | 41.43 | 34.46 | 55.31 | |
| 200 | 42.78 | 26.60 | 67.71 |
| Плита / горячая точка | Возраст | φ | λ | ω |
| Гренландия / горячая точка | 20 | 13.72 | 26.03 | 4.57 |
| 40 | 40.96 | 113.53 | 5.08 | |
| 60 | 42.10 | 88.32 | 11.77 | |
| 80 | 20.79 | 86.07 | 17.81 | |
| 100 | 32.67 | 84.19 | 23.18 | |
| 120 | 41.97 | 73.88 | 31.09 | |
| 140 | 43.94 | 65.94 | 36.32 | |
| 160 | 49.45 | 50.51 | 49.52 | |
| 180 | 52.58 | 36.71 | 64.56 | |
| 200 | 52.72 | 26.39 | 76.35 |
| Плита / горячая точка | Возраст | φ | λ | ω |
| Антарктида / горячая точка | 20 | -38.46 | 5.15 | 6.28 |
| 40 | -86.61 | 260.78 | 7.00 | |
| 60 | -88.09 | 251.84 | 7.14 | |
| 80 | -64.67 | 43.72 | 7.86 | |
| 100 | -62.90 | 349.66 | 13.49 | |
| 120 | -55.11 | 335.59 | 22.85 | |
| 140 | -35.47 | 325.92 | 30.22 | |
| 160 | -26.61 | 336.30 | 32.53 | |
| 180 | -15.99 | 343.92 | 38.31 | |
| 200 | -5.92 | 352.01 | 48.43 |
| Плита / горячая точка | Возраст | φ | λ | ω |
| Австралия / горячая точка | 20 | -43.30 | 230.99 | 9.32 |
| 40 | -26.69 | 211.96 | 24.90 | |
| 60 | -23.72 | 207.56 | 33.26 | |
| 80 | -25.72 | 204.91 | 30.12 | |
| 100 | -37.01 | 211.97 | 31.71 | |
| 120 | -50.55 | 223.90 | 35.39 | |
| 140 | -50.00 | 253.22 | 37.93 | |
| 160 | -50.87 | 268.40 | 34.00 | |
| 180 | -46.59 | 292.92 | 31.80 | |
| 200 | -34.05 | 321.61 | 32.68 |
| Плита / горячая точка | Возраст | φ | λ | ω |
| Индия / горячая точка | 20 | -43.30 | 230.99 | 9.32 |
| 40 | -26.69 | 211.96 | 24.90 | |
| 60 | -25.48 | 191.30 | 42.42 | |
| 80 | -19.70 | 184.13 | 62.12 | |
| 100 | -17.62 | 185.85 | 71.64 | |
| 120 | -17.42 | 186.46 | 77.87 | |
| 140 | -21.28 | 187.04 | 74.07 | |
| 160 | -20.38 | 188.04 | 67.08 | |
| 180 | -19.94 | 190.78 | 57.82 | |
| 200 | -18.23 | 194.86 | 44.49 |
Задача 39. Используя данные задачи 33, определить координаты точек Евразиатской плиты на время 83 млн лет назад относительно Североамериканской плиты: а) Мадрид (40°с.ш.,4°з.д.); б) Мурманск (69°с.ш.,33°в.д.); в) Магнитогорск (50°с.ш., 59°в.д.).
Ответ: а) 41,58°с.ш., -28,83°з.д.; б) 73,92°с.ш., -0,09°з.д.; в) 59,61°с.ш., 37,79°в.д.
Задача 40. Используя данные задачи 33, определить координаты точек Североамериканской плиты на время 83 млн лет назад относительно Евразиатской плиты: а) Сен-Джонс (48°с.ш., -53°з.д.); б) Бэрроу (Аляска) (72°с.ш., -150°з.д.); в) Сан-Франциско (38°с.ш. -122°з.д.); г) Майами (26°с.ш., -80°з.д.).
Ответ: а) 49,15°с.ш., -26.30°з.д.; б) 77,67°с.ш., -150,59°з.д.; в) 44,68°с.ш., -102,03°з.д.); г) 30,26°с.ш., -58,04°з.д.
Задача 41. Используя таблицу задачи 37: а) определить координаты г.Касабланки (Африканская плита) (современные координаты 33°с.ш., -8°з.д.) на время 127 млн лет назад при перемещении ее относительно Североамериканской плиты; б) определить расстояние между Касабланкой и Нью-Джерси (39°с.ш., -74°з.д.) в современных координатах и на время 127 млн лет назад.
Ответ: а) 35,94°с.ш., -44,97°з.д.; б) 5841 км, 2572 км.
Задача 42. Используя таблицу из задачи 38, определить угловую скорость движения Индии относительно горячей точки на этапе 80-40 млн лет назад. Какова линейная скорость точки 18°с.ш., 72°в.д.) г.Бомбей в этом интервале времени?
Ответ: 1,04°/млн лет; 11,1 см/год.
Задача 43. Используя таблицу из задачи 38, определить координаты горячей точки (современное положение), если известно что траппы Деканского плато (Индийская плита) (современные координаты 19°с.ш., 76°в.д.) изливались 64 млн лет назад.
Ответ: -17,54°ю.ш., 56°в.д. (близко к современным горячим точкам Реюньон и Маврикий
Задача 44. Используя данные задачи 37, определить параметры конечного движения Южной Америки относительно Северной Америки на этап 83 млн лет.
Ответ: полюс 8,4°с.ш., 33,9°в.д.; ω = 9,28°.
Задача 45. Определить угловую скорость вращения Гренландии относительно Северной Америки на время 60 млн лет назад, используя таблицу из задачи 37.
Ответ: 0,37°/млн лет вокруг полюса 66,2°с.ш., -100,54°з.д. ).
Глава 2. Палеомагнитные методы палинспастических реконструкций
Горные породы находятся в магнитном поле Земли. Если в них содержатся магнитные минералы (а почти все минералы обладают магнитными свойствами), то они намагничиваются в соответствии с существующим магнитным полем. Более того, выяснилось, что в горных породах часто сохраняется их первичная намагниченность, возникшая в период их образования. Эта намагниченность, называемая остаточной, выявляется путем сложных физических изменений, но именно она является предметом исследования палеомагнитологии
Остаточная намагниченность включает много составляющих в разные моменты времени и часто значительно разрушенных. Измерения палеомагнитологов напоминают работу археологов, вынужденных пласт за пластом снимать наслоение более поздней намагниченности, чтобы Наконец получить исходную остаточную намагниченность пород.
Конечно, вся работа основана на трех важных допущениях: во-первых, горные породы действительно намагничиваются по направленно геомагнитного поля времени их образования; во-вторых, первичная намагниченность действительно сохраняется; в-третьих, геомагнитное поле является полем диполя с осью, совпадающей с осью вращения Земли (гипотеза осевого диполя). Как показывают многочисленные данные, все три допущения являются справедливыми. Однако и кратковременные (десятки тыс.лет) периоды инверсий магнитное поле Земли не является осевым диполем.
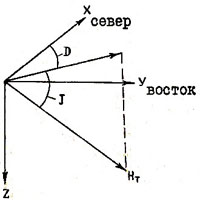
Рис. 29. Основные элементы земного магнетизма.
D – склонение геомагнитного поля; J – наклонение геомагнитного поля; Ht – полный вектор напряженности магнитного поля
Магнитное поле описывается вектором, отвечающим ориентировки ммгнитных силовых линий. Вектор раскладывается на две составляющие (рис.29): горизонтальную, называемую склонением, и вертикальную, называемую наклонением. На экваторе наклонение равно 0, на полюсе – 90°.
Задача палеомагнитных исследований сводится к отысканию палеосклонения и палеонаклонения вектора остаточной намагниченности горной породы. Для этого берутся ориентированные образцы, производится их обработка (как говорят, чистка) и измеряется вектор остаточной намагниченности. Используя замеренные склонения и наклонения, рассчитывается положение на земной сфере палеомагнитного полюса.
Географические координаты – широта Φ и долгота Λ – палеомагнитного полюса рассчитываются. Если в точке с географическими координатами – широтой φ и долготой λ – известны значения склонения D и наклонения J, то
sinΦ = sinφ*sinφm+cosφ*cosφm*cosD
sinΦ = cosφm*sinD/cosΦ
Φ = Λ − λ , если sinφm>e;sinφ*sinΦ
Φ = 180 − (Λ − λ), если sinφm<sinφ*sinΦ
φm – палеомагнитная широта, определяемая по формуле
tgφm= 0,5 tg J .
Если бы континенты (вместе с литосферными плитами) не перемещались, а оставались бы постоянно в одном месте на земной сфере, то палеомагнитные полюса всегда в среднем находились вблизи современных географических полюсов. Однако в действительности этого почти никогда не наблюдается. Например, палеомагнитный полюс для Сибирской платформы, определенный по породам каменноугольного возраста, имеет координаты 30°с.ш., 150°в.д. и находится в Тихом океане, а для пермского периода – 45°с.ш., 144°в.д. – и находится в Японском море.
Определяя палеомагнитные полюса для конкретных моментов геологического времени, палеомагнитологи получают серию последовательных положений палеомагнитного полюса относительно каждого континента (или любого выбранного блока коры). Нанося на карту координаты палеомагнитных полюсов для разных моментов времени и соединяя их условно линиями, получаем кривые кажущейся миграции палеомагнитных полюсов.
Можно, конечно предположить, что континенты остаются на месте, а перемещаются палеомагнитные полюса. Но в этом случае палеомагнитные полюса и, значит, кривые кажущейся миграции палеомагнитных полюсов для разных континентов долкны совпадать (хотя бы в первом приближении, учитывая ошибки в смещениях).
Можно взять данные из таблицы к задаче 37 и убедиться в том, что кривые кажущейся миграции совершенно не совпадают. Скажем для того же каменноугольного и пермского периодов, которые взяты в качестве примера для полюсов Сибири, палеомагнитнне полюса Северной Америки имеют координаты соответственно 34°с.ш., 128°в.д. и 44°с.ш., 118°в.д. Такое несовпадение палеомагнитных полюсов служит надежным подтверждением широкомасштабного дрейфа континентов.

Рис. 30. Прошлое распространение верхнепалеозойских комплексов. Стрелками показаны направления на палеомагнитный полюс. Цифры – палеошироты. Заштрихованы океаны, точки – шельфовые моря

Рис. 31. Распространение ледниковых отложений (точки), красноцветов и солей (лодочки), рифовых известняков (клетки), углей (черные штрихи) при современном положении континентов. Каждый из комплексов маркирует свой климатический пояс (полярный, тропический, аридный, экваториальный и умеренный гумидный)
Палеомагнитные результаты могут быть подтверждены независимыми данными. Главными из них являются палеоклиматические данные. Приведем лишь один пример. На рис.30 показано положение палеомагнитных векторов для главных континентов для пермского времени (280 млн лет назад) и распространение геологических комплексов-индикаторов прошлого климата: ледниковых отложений, тропических известняков, аридных солей и др. Не трудно видеть полное несоответствие с современными широтами, В Евразии, скажем, все палеомагнитные векторы ориентированы широтно, а не меридионально, как им положено. В Африке, Индии и Австралии, в районах, близких к экватору, значения палеоширот равны 40 – 50°ю.ш.
Верхнепалеозойские ледниковые отложения также распространены сейчас вблизи экватора, а тропические известняки, напротив, в высоких широтах Северного полушария. Все эти противоречия полностью снимаются, если принять реконструкцию Пангеи (сделанную еще в начале XX в. Альфредом Вегенером). Существует полное согласие между палеомагнитными и палеоклиматичесними данными; это лишний раз убеждает, что движутся не полюса, а материки (рис.31).
Палеомагнитные данные являются количественным показателем движения плит, причем для палеозойского и более раннего времени пока единственным количественным методом, позволяющим оценивать перемещение не на глаз, а числом. Если известно для какой-то точки, что в момент времени t1 ее палеоширота была равна φ1, а во время t2 она составила φ1, то величина перемещения будет равна φ2-φ1. Одновременно измеряется и склонение D. Разница в склонениях D2-D1 дает величину разворота континента (или иного блока) относительно земного меридиана. Например, 280 млн лет назад данная точка была на 10°с.ш. и палеосклонение в ней составляло 25°, а 200 млн лет назад она оказалась на 40°с.ш. и палеосклонение стало 50°, то блок в данной точке сместился на 30° по дуге большого круга на север (1° – 111 км, следовательно на 3330 км) и развернулся на 25° по часовой стрелке. Заметим, что палеомагнитные данные определяют перемещение только поперек широт, дают тем самым только широтную составляющую движения плит. Они никак не указывают на перемещение поперек долгот. Истинные перемещения блоков могут быть только большими, чем широтная составляющая.
Вся процедура палеомагнитных измерений, несмотря на высокое качество аппаратуры, сопровождается определенными погрешностями. Нет уверенности в достоверности определения возраста намагниченности, или в том, не происходило ли более позднее перемагчивание, какие минералы являются носителями намагниченности и когда они образовались. Поэтому любое определение палеомагнитного полюса проводится с той или иной степенью вероятности.
Задача 46. В точке с координатами 41,5°с,ш., 72,73°в.д. измерены склонение и наклонение палеомагнитного полюса по намагниченности пород верхнего триаса (D=I8°, J=12°). Определить координаты палеомагнитного полюса для позднего триаса.
Ответ: Φ=51,1°с.ш., Λ=223,4°з.д., φm=6,07°.
Задача 47. Измерены склонение и наклонение палеомагнитного полюса в породах олигоцена в точке с координатами 51°с.ш., 14,7°в.д.; D=200°, J=-63°. Определить координаты палеомагнитного полюса.
Ответ: Φ=75°ю.ш., Λ=-57,05° .д., φm=-44,46°.
Задача 48. В точке с координатами 45,5°с.ш. и 73°в.д. измерены склонение D=154° и наклонение палеомагнитного полюса φ=-58°. Найти положение палеомагнитного полюса.
Ответ: Φ=69,63°ю.ш., Λ=152°в.д., φm=-38,67°.
Задача 49. В точке А (65°с.ш., 165°в.д.), находящейся на Омолонском массиве, вектор магнитного поля в триасовых отложениях имеет следующие характеристики: D=300°, φ=70°. Найти положение палеомагнитного полюса. Оценить и дать характеристику движений блока от триаса до современного положения.
Ответ: Φ=59°с.ш., Λ=83,4°в.д., φm=54°с.ш.
Задача 50. В точке А (65°с.ш., 165°в.д.), находящейся на Омолонском массиве, палеомагнитный вектор для триаса имеет следующие характеристики по отношению к Сибири: D=150°, J=80°. Определить расстояние по широте между Омолонским массивом и
Сибирским континентом. Каким было движение Омолонского массива относительно Сибири?
Ответ: Φ=47,14°с.ш., Λ=179,1°в.д., φm=70,6°с.ш.
Задача 51. В точке Омолонского массива А (65°с.ш., 165°в.д палеомагнитный вектор в юрских отложениях имеет следующие характеристики: D=270°, J=75°. Определить историю движения блока от триаса до юры и от юры до современного положения.
Ответ: Φ=53°с.ш., Λ=113,25°в.д., φm=6I,8°c.ш.
Задача 52. Даны средние палеомагнитные полюсы для крупных литосферных плит (по А.Н.Храмову). Проанализировать движение литосферных плит в фанерозое.
| Подразделения геохронологической шкалы | Палеополюс | |
| Φ ° | Λ ° | |
| Восточно-Европейская плита | ||
| 76 | 162 | |
| K | 77 | 180 |
| J | 74 | 167 |
| T2-3 | 55 | 137 |
| T1 | 51 | 152 |
| P2 | 45 | 162 |
| P1 | 40 | 167 |
| C3 | 41 | 169 |
| C2 | 32 | 163 |
| C1 | 46 | 158 |
| D1 | 31 | 161 |
| S-D | 5 | 134 |
| S1 | 38 | 155 |
| O | 30 | 143 |
| -13 | 135 | |
| Подразделения геохронологической шкалы | Палеополюс | |
| Φ ° | Λ ° | |
| Восточно-Сибирская плита | ||
| K | 74 | 180 |
| T2-3 | 59 | 137 |
| T1 | 49 | 149 |
| P | 45 | 141 |
| C1-2 | 30 | 150 |
| D3 | 20 | 140 |
| D2 | 15 | 116 |
| D1 | -10 | 104 |
| O3 | -21 | 131 |
| O2 | -24 | 132 |
| O1 | -42 | 134 |
| -36 | 126 | |
| -39 | 156 | |
| -54 | 208 | |
| Подразделения геохронологической шкалы | Палеополюс | |
| Φ ° | Λ ° | |
| Северо-Американская плита | ||
| 86 | 223 | |
| K2 | 70 | 206 |
| K1 | 70 | 184 |
| J1-K1 | 66 | 187 |
| J | 68 | 140 |
| T2-3 | 64 | 91 |
| T1 | 53 | 107 |
| P2 | 52 | 114 |
| P1 | 44 | 118 |
| C3 | 37 | 124 |
| C1-2 | 34 | 128 |
| D | 44 | 122 |
| S | 29 | 123 |
| S-D | 22 | 120 |
| O2 | 33 | 138 |
| O1 | -19 | 126 |
| -16 | 176 | |
| 13 | 155 | |
| 40 | 131 | |
| Подразделения геохронологической шкалы | Палеополюс | |
| Φ ° | Λ ° | |
| Южно-Американская плита | ||
| K | 82 | 228 |
| J | 83 | 254 |
| T2-3 | 77 | 86 |
| P2-T1 | 74 | 45 |
| P2 | 75 | 135 |
| P1 | 62 | 170 |
| C3 | 53 | 164 |
| O-D | -1 | 127 |
| -13 | 154 | |
| -29 | 214 | |
| P | -26 | 139 |
| Подразделения геохронологической шкалы | Палеополюс | |
| Φ ° | Λ ° | |
| Индийская плита | ||
| 72 | 249 | |
| 45 | 283 | |
| 37 | 278 | |
| К2- | 33 | 281 |
| К2 | 33 | 280 |
| К1 | 19 | 298 |
| J | 14 | 295 |
| T3 | 20 | 308 |
| P2-T1 | -5 | 307 |
| T1-2 | 29 | 206 |
| Подразделения геохронологической шкалы | Палеополюс | |
| Φ ° | Λ ° | |
| Африканская плита | ||
| 82 | 111 | |
| 77 | 177 | |
| К2 | 71 | 212 |
| К1 | 60 | 253 |
| J | 67 | 258 |
| T | 67 | 265 |
| P1 | 38 | 245 |
| C1-2 | 21 | 211 |
| D3 | 0 | 205 |
| -14 | 156 | |
| -27 | 165 | |
| Подразделения геохронологической шкалы | Палеополюс | |
| Φ ° | Λ ° | |
| Австралийская плита | ||
| 74 | 276 | |
| 66 | 312 | |
| К | 54 | 327 |
| J | 48 | 343 |
| Т | 49 | 330 |
| P2 | 42 | 307 |
| C3 | 49 | 319 |
| C2 | 42 | 307 |
| D1 | 82 | 306 |
| S2-D3 | 70 | 162 |
| S | 44 | 82 |
| 13 | 212 | |
| 7 | 161 | |
| P | -28 | 158 |
| Подразделения геохронологической шкалы | Палеополюс | |
| Φ ° | Λ ° | |
| Антарктическая плита | ||
| Р | 81 | 237 |
| К | 80 | 279 |
| J | 54 | 36 |
| Т | 50 | 29 |
Геоисторический анализ линейных магнитных аномалий в океане
Установлено, что аномальное магнитное поле океана имеет линейный рисунок: положительные и отрицательные аномалии одинаковой амплитуды чередуются между собой, причем их расположение оказывается симметричным относительно современных (или прошлых) осей спрединга океанского дна. Ф.Вайн и Д.Мэтьюз объяснили эту картину тем, что положительно и отрицательно (прямо и обратно) намагниченные полосы отвечают участкам коры, формировавшимся в осях спрединга соответственно в периоды прямой или обратной намагниченности, разделенные моментами инверсий геомагнитного поля. Поскольку каждый период той или иной полярности имел свою продолжительность и свои характерные особенности, удалось связать шкалу инверсий и порядок расположения линейных магнитных аномалий хронологической шкалой. Аномалии были пронумерованы а каждая из них бала привязана к возрастной шкале (эта привязка постоянно совершенствуется).
Существование линейных магнитных аномалий является решающим при выяснении количественной стороны движения литосферных плит. Уже говорилось, что только измерения расстояний между аномалиями, для которых известен возраст, позволяют определить скорость движения литосферных плит. Столь же большое значение имеет расположение магнитных аномалий для выяснения истории двяжения литосферных плит. Поэтому говорят о необходимости их "геоисторического" анализа. В основе тектоники плит лежит то, что линейные аномалии отвечают возрасту ложа океанов и то, что они отвечают осям спрединга соответствующего времени.

Рис. 32. Примеры геоисторического анализа линейных магнитных аномалий
Три примера, приведенные на рис. 32, помогут понять, как производится геоисторический анализ спрединга.
Пример 1 (рис.32,а). В океане между континентами А и В прослеживается система симметричных магнитных аномалий от No.I9 (4 млн лет) до современной оси спрединга. Палеотектоническая история проста: примерно 45 млн лет назад произошел раскол континента на плиты А и В и между ними образовался океанский бассейн. Мы вправе ожидать хорошо развитые пассивные окраины с мощными призмами осадков – вместилищем залежей нефти и газа.
Пример 2 (рис.32,б). Четыре континентальных блока А, В, С и Д разделены океанскими бассейнами. В них выявлено две разновозрастные системы линейных магнитных аномалий: более древняя с 13 по 7 и более молодая с 6 до современной оси спрединга. Естественно, что более молодая система пересекает более древнюю, История распадается на два этапа. В первый из них единый континент, включавший все четыре блока – А, В, С и Д, подвергся расколу вдоль СЗ оси спрединга. Спрединг начался чуть раньше 37 млн лет, а закончился между временем аномалий 7 и 6, т.е. между 26 и 20 млн лет. В это время существовало две плиты: АС и БД. Второй этап начался с принципиальной реорганизации: северо-западная ось спрединга отмерла, и возникла поперечная северо-восточная ось спрединга. Образовались две новые плиты: АВ и СД. Эволюция показана в правой части рисунка (стадии с I по 4).
Пример 3. Зона субдукции отделяет континентальную плиту К от океанической плиты А. На океанской плите есть коленобразно изогнутая система линейных магнитных аномалий от 13 до 32 (от 37 до 70 млн лет). Если мы попытаемся представить, какая геодинамическая ситуация существовала на время, близкое к аномалии 13, то получим картину, изображенную (уменьшено) на правой стороне рисунка (рис.32,в). В это время было три оси спрединга, разделявшие три плиты: А, В и С. Из этих трех плит в результате субдукции были полностью поглощены плиты С и Д, и осталась лишь плита А. Этот пример показывает, что анализ магнитных аномалий позволяет восстанавливать не только прошлое взаимодействие, но даже исчезнувшие плиты, полностью поглощенные в зонах субдукции.
Анализ линейных магнитных аномалий океана – увлекательное занятие, он напоминает восприятие тектонистом геологической карты; в рисунке аномалии запечатлена жизнь океанского дна с казалось бы небыстрым движением, но приводящим зачастую к драматическим событиям.
Литература
Глава 3. Тектонические карты и их составление
По сравнению с геологическими, тектонические карты дают возможность более полно, с привлечением дополнительной информации, изобразить поверхностную и глубинную структуру, а также происхождение рассматриваемого участка земной коры. В зависимости от масштаба и назначения, а также от изображаемого на нах объекта, они весьма разнообразны. Наряду с тектоническими картами обычного типа (региональными и обзорными), составляют так называемые геодинамические, а также различные специализированные тектонические карты. Особой категории принадлежат палеотектонические карты.
Региональные и обзорные тектонические карты
При составлении тектонических карт обычного типа наглядное отражение структуры должно сочетаться с обозначением тентонической природы выделяемых структурных единиц, времени и последовательности их формирования. Поэтому их содержание в большой степени зависит от трактовки, которую дают ее авторы исходя из той или иной теоретической концепции, а также в зависимости от принятых ими тектонических решений. Создание региональной тектонической карты (от масштабов 1:25 000 до 1:500 000 и 1:1 000 000) предусматривает в каждом случае разработку таких условных обозначений и изобразительных средств, которые могли бы наилучшим образом раскрыть характерные особенности тектоники рассматриваемой территории. Это не исключает применения единой системы условных обозначений для серии карт в пределах определенной тектонической зоны или области. При переходе от региональных к обзорным тектоническим картам континентального и глобального масштаба неизбежна унификация главных характеристик и условных обозначений.
На континентальных шельфах, при наличии достаточных данных, тектоника изображается почти теми же средствами, что и на территории континентов. Коренным образом отличаются тектонические карты областей с океанским типом коры, а также расположенных в зонах перехода континент/океан.
Изображение тектонической структуры
В складчатых областях крупные структурные формы изображаются либо выделением структурных этажей (и подэтажей), либо, в случае шарьяжного строения, выделением тектонических покровов. Обычно границами структурных этажей служат главные стратиграфические несогласия – угловые и азимутальные. В результате карта, на которой выделены (чаще всего цветом) * Те же структурные единицы иногда выделяют под названием структурных ярусов и подъярусов. Термин "структурный комплекс" применяется в разных значениях, в том числе как совокупность нескольких структурных этажей. структурные этажи и подэтажи*, представляет собой определенным образом генерализованную геологическую карту. На ней в обобщенном виде различимы синклинории, антиклинории и другие крупные формы складчатой структуры.
При прослеживании структурных этажей или подэтажей из одой части территории в другую (особенно при переходе из одной тектонической зоны в другую) нередко обнаруживается некоторое изменение времени формирования разделяющего их несогласия: оно может скользить вверх или вниз по геохронологической шкале, или же резко, скачкообразно менять свое стратиграфическое положение. Такие соотношения придают условность прослеживанию единых структурных этажей или подэтажей по всей рассматриваемой территории и обычно поясняются в условных обозначениях тектонической карты.
В случае шарьяжного строения цвет используется в первую очередь для выделения автохтона (а также, если нужно, паравтохтона) и аллохтонннх единиц: тектонических покровов и их более дробных подразделений: пластин, чешуй, скиб, дигитаций и т.д. Это позволяет прочитать на карте не только собственно марьяжную структуру, но и последующие крупные деформации тектонических покровов – как складчатые (антиформы и синформы), так и разрывные. Подошва тектонических покровов трассируется поверхностями надвигов, зонами тектонического меланжа или базальными олистостромовыми горизонтами.

Рис.33. Условные обозначения складок и разрывов: а – оси линейных складок: антиклинальных и синклинальных; а – то же для опрокинутых складок (стрелка – по падению осевой поверхности); б – менее наглядные обозначения осей линейных складок; в – брахиморфные антиклинали и синклинали, купола и мульды; г – сбросы (штрихи по падению сместителя); д – взбросы; е – сдвиги; ж – крутые разрывы с неустановленным характером смещения; з – надвиги (значки в направлении аллохтона)
Таким образом, выделение структурных этажей (подэтажей) или тектонических покровов выражает на карте крупные структуры складчатого сооружения, на фоне которых дополнительными знаками дается изображение более мелких структурных форм. На рис. 33 даны наиболее распространенные условные обозначения линейных и брахиморфных складок, главных видов разрывных нарушений. Для линейных складок наиболее нагляден знак "а"; знак "б" рекомендуется использовать как дополнительный в том случае, если на одной и ной же карте нужно различать линейные складки разной морфологии или разного масштаба. При изображении сбросов и взбросов (знаки "г" и "д") штрихи должны быть направлены по падению поверхности сместителя. При проведении надвигов зубчики должны быть направлены в сторону аллохтона, независимо от современного наклона сместителя, который нередко бывает обусловлен последующими изгибами тектонических покровов и пластин. При пологом залегании слоев в верхних структурных этажах складчатых сооружений или в межгорных и передовых прогибах, для изображения структуры иногда используются системы стратоизогипс или знаки моноклинального залегания. Здесь, как и на крыльях линейных и брахиморфных складок, уместно нанесение наиболее характерных элементов залегания слоев с указанием угла падения.
При наличии результатов дешифрирования аэрофотоматериалов или космических снимков может возникнуть необходимость нанесения на тектоническую карту линеаментов и иных, в том числе кольцевых структурных форм, нередко не картируемых на местности и не имеющих выражения на геологической карте.
На платформах и срединных массивах характеристика структуры предусматривает изображение глубин залегания фундамента, внутренней структуры чехла и внутренней структуры фундамента. Глубина залегания фундамента (его тектонический рельеф) строится на основании сейсмических и буровых данных и изображается на карте либо изолиниями, либо густотой окраски чехла: чем ближе к поверхности фундамент, тем интенсивнее цвет. Строение плитформенного чехла обычно отображается в стратоизогипсах. При наличии в чехле нескольких структурных этажей дается несколько систем стратоизогипс, для распознавания которых вводятся условные обозначения. В районах, где платформенный чехол деформирован и частично эродирован, возможно наглядное изображение структурных этажей цветом по их выходам на поверхность (т.е. путем генерализации геологической карты). Более дробные элементы структуры чехла – флексуры, купола, валы, впадины, разрывы – даются дополнительными знаками.
Строение фундамента платформ и срединных массивов (чаще всего это сложные складчатые и метаморфогенные структуры) возможно изобразить главным образом там, где этот фундамент выходит на поверхность. Попытки показать строение фундамента под структурами чехла (при наличии необходимой информации) приводят к перегрузке тектонической карты.
Генетическая нагрузка тектонических карт
Как уже отмечалось, содержание тектонических карт предусматривает основную информацию об истории тектонического развитии рассматриваемой территории, что отличает эти карты от структурных.
В складчатых областях давно уже проводится районирование по времени главной ("завершающей") складчатости. На обзорных тектонических картах СССР и крупных его частей выделялись окраской альпиды, мезозоиды, герциниды, каледониды, и области докембрийских эпох складчатости (см. Тектоническую карту СССР масштаба 1:5 000 000, 1956 под редакцией Н.С.Шатского и более поздние карты того же типа). Этот принцип до настоящего времени широко применяется и для региональных карт, на которых уточняется возраст главной складчатости, и соответствующее деление складчатой области дается более дробно. Б некоторых случаях вводятся специальные обозначения для тех участков складчатых систем, которые испытали существенную тектоническую переработку в одну из последующих эпох складчатости. В метаморфических комплексах иногда приходится датировать на столько главную складчатость, сколько главную фазу метаморфизма или тектономагматического преобразования пород.
Генетическая нагрузка таких карт дополняется выделением показательных в отношении тектонического режима формаций, таких как флиш, моласса, офиолиты, орогенные гранитоиды и т.д. Обычно дается и трактовка разломных зон, выделяются наиболее важные глубинные разломы, сутуры, а в покровно-складчатых сооружениях – главные поверхности шарьирования.
В пределах платформ и срединных массивов возраст складчатого основания показывается окраской чехла. В частности на обзорных картах по-разному окрашены области с докембрийским фундаментом ("древние платформы") и палеозойским фундаментом ("молодые платформы"). На региональных картах возраст фундамента дается подробнее, а размещение и взаимоотношение структурных этажей чехла позволяет судить о развитии платформенных бассейнов: их раздвигании, сокращении, смещении, переориентировке и т.д.
В конце семидесятых годов были созданы региональные тектонические карты Урала, Северо-Востока СССР, Восточного Казахстана, а также обзорная Тектоническая карта Северной Евразии масштаба 1:5 000 000 (под редакцией А.В.Пейве и А.Л.Яншина, 1979), на которой районирование определялось не возрастом главной складчатости, а "временем становления коры континентального типа". В основу была положена разработанная в Геологическом институте АН СССР схема стадийного развития: от океанской стадии к переходной (с господством островодужных обстановок), а затем – континентальной. Предполагалось, что континентальная кора складчатых областей фанеророзоя – новообразование, сформировавшееся таким способом за счет коры океанской. На этих картах окраска обозначает определяемое авторами время становления гранитно-метаморфического слоя коры, оттенки – структурно-формационные комплексы, отвечающие стадиям процесса, а крапы и штриховки – осадочные, вулканические и интрузивные формации, образующие эти комплексы.
Во многих складчатых областях отчетливо выражена и должна быть показана на тектонических картах (особенно средне- и крупномасштабных) структурно-формационная (тектоническая) зональность. Как правило, такие зоны линейны, она различаются интервалом и полнотой стратиграфического разреза, характером осадочных и магматических формаций, а также особенностями складчатости и метаморфизма, временем их проявления. При шарьировании комплексы структурно-формационных зон обычно образуют самостоятельные тектонические покровы, однако известны и такие шарьяжяые единицы, в состав которых вошли породы двух или более соседних тектонических зон. Поверхность надвига в этом случае не совпадает с границей тектонических зон, она пересекает ее под более или менее острым углом. При необходимости тектонические зоны делят на подзоны. Тектоническим зонам обычно дается географическое название, которое может сопровождаться определением, отражающим особенности строения и происхождения зоны, ее положение в складчатом сооружении ("пологоскладчатая зона", "флишевая зона", "центральная зона" и т.д.). Несколько тектонических зон могут объединяться, образуя более крупные подразделения складчатой области: складчатые системы, срединные массивы, межгорные и передовые прогибы и др.
При определении происхождения тектонических зон и их сочетаний в настоящее время используются новые возможности, основанные на актуалистическом подходе с учетом всей совокупности геолого-геофизических, геохимических и прочих данных о глубинных условиях и поверхностном проявлении современного тектогенеза, как и активных поясах на границе литосферных плит, так и внутриплитного. При таком подходе в основу тектонической карты может быть положено выделение геологических комплексов, отвечающих главным геодинамическим обстановкам. Такие карты называют геодинамическими. Примером может послужить изданная в 1990 г. Геодинамическая карта СССР масштаба 1:2 500 000 (под редакцией Л.П.Зоненшайна, Н.В.Межеловского, Л.М.Натапова), на которой цвет использован для обозначения комплексов (осадочных, вулканических, интрузивных, метаморфических), формировавшихся в океанских и континентальных рифтовых зонах, в островодужных и окраинно-континентальных зонах субдукции, в коллизионных зонах, на пассивных континентальных окраинах и во внутренних частях континентов и океанов. Оттенок цвета позволит различать однотипные комплексы разного возраста. Более дробное деление комплексов дано на карте с помощью крапов и штриховок. Наряду с традиционными элементами структурами показаны линии перехода древних зон субдукции, тектонический меланж, аккреционные призмы и др. Нанесены (с указанием возраста) палеомагнитные векторы и полюсы вращения плит.
Важным структурным элементом многих складчатых областей являются так называемые экзотические террейны: микроконтиненты, фрагменты островных дуг или внутриокеанских поднятий, приченившихся к активной континентальной окраине в ходе длительной субдукции и таким образом включенные, как инородное тело, в складчатую область. Геодинамические карты, особенно среднемасштабные, позволяют показать такие террейны и обозначить их вероятное происхождение. Примером могут служить экзотические террейны Северо-Востока СССР и Малого Кавказа. На мелкомасштабных картах ограничиваются суммарным изображением всей совокупности, коллажа террейнов.
В наиболее сложных шовных (сутурных) зонах складчатых областей бывают тектонически сближены весьма разнообразные геодинамические комплексы. Таковы, в частности, многие офиолитовые зоны, этом случае необходимо и возможно составление геодинамических карт детальных масштабов. На таких картах геодинамические комплексы могут быть расчленены, а их структурные взаимоотношения и внутренняя структура показаны гораздо подробнее. Так, например, пределах комплекса океанских рифтов раздельно изображаются серпентинизированные и тектонизированные гипербазиты мантии, расслоенные гипербазит-базитовые серии, пакеты параллельных долеритовых даек, излившиеся базальты, радиоляриты, метаморфиты и т.д. При детальном масштабе в тектоническом меланже различимы слагающие его элементы и включения, а в олистостромах – крупные олистолиты разного состава. Геодинамические карты находят в последние годы всё более широкое применение, в том числе для целей металлогенического прогноза.
Специализированные тектонические карты
Как для решения практических задач, так и в связи с научными исследованиями составляются специализированные тектонические карты, на которых дается информация узкого целевого назначения. На обычных тектонических картах эта информация как правило, почти отсутствует. Специализированные карты так же разнообразны, как и задачи, для которых они составляются. С появлением новых задач разрабатываются и новые типы карт. Их масштабы – от детальных до глобальных.
Сведения о современных движениях земной коры представлены на картах современных вертикальных движений (которые составляются главным образом по данным повторных нивелировок), а также на картах современной кинематики литосферных плит и микроплит, где даны векторы современных горизонтальных движений. При составлении карт мгновенной кинематики учитываются решения фокального механизма сейсмических очагов, определения скоростей спрединга по самым молодым линейным магнитным аномалиям, повторные промеры расстояний между удаленными точками с помощью спутниковых лазерных отражателей и посредством радиоинтерферометрии. Детальные карты современных горизонтальных движений составляют для территории полигонов где проводится повторная лазерная трилатерация. Для целей сейсмического прогноза строят сейсмотектонические карты.
Карты новейших вертикальных движений земной коры континентов составляют главным образом на основе геоморфологических методов, примером может служить Карта новейшей тектоники СССР и сопредельных территорий масштаба 1:5 000 000, 1982 г. под редакцией Н.И.Николаева. Изображение горизонтальных движений новейшего времени требует составления палеотектонических карт (см. ниже).
Целый ряд специализированных карт предназначен для более полного изображения тектонической структуры, выявления тех или иных ее особенностей. Таковы структурные карты, на которых все графические средства используются для более детального изображения структуры, чем это возможно на обычных тектонических картах. Составляются карты разломов, такие как изданная Карта разломов территории СССР масштаба 1:2 500 000, 1978 г. под редакцией А.В. Сидоренко. С использованием съемок из космоса создаются космотектонические карты, карты линеаментной тектоники, карты кольцевых структур. В числе таких карт – Космогеологическая карта линеаментов и кольцевых структур территории СССР масштаба 1:5 000 000, I960 г. под редакцией А.Д.Щеглова. Строение нижних структурных этажей и глубоких частей земной коры дается на тектонических картах со снятым чехлом тех или иных отложений, на тектонических картах фундамента, (например на Тектонической карте фундамента территории СССР масштаба 1:5 000 000, 1974 г. под редакцией Д.В. Наливкина), а также на картах глубинного строения земной коры.
В качестве карт, предназначенных непосредственно для поисково-разведочных работ на полезные ископаемые, можно назвать карты рудоконтролирующих структур, а также тектонические карты нефтегазоносных областей. На последних основное внимание уделяется выявленным в осадочном чехле нефтегазоносных областей структурам разного масштаба и типа.
Палеотектонические карты
Если палеогеологические карты во всем подобны современным геологическим (давая такое же изображение для древнего, ныне погребенного среза), то отличие палеотектонических карт от тектонических более существенно. В основе обычных тектонических карт, как было показано выше, лежит изображение современной структуры земной коры, которая как правило представляет собой суммарный результат многократных и разнообразных тектонических движений и деформаций. Палеотектоническая карта – это реконструкция тектонической обстановки для какого-то ограниченного отрезка времени ("момента" геологической истории). В большинстве случаев создание ее требует возвратного горизонтального перемещения геологических тел (литосферных плит и разнообразных террейнов, а также смещенных по сдвигу блоков земной коры или шарьированных тектонических покровов) с тем, чтобы восстановить их взаимное расположение в соответствующий момент времени. Эта процедура, называемая, как уже отмечалось выше, палинспастической реконструкцией, основывается на учете картируемых структурных взаимоотношений (см.рис.6,II), закономерностей нормального размещения фациальных комплексов (см.рис.3). Все большее значение приобретает применение палеомагнитных методов: данных об ориентировке векторов остаточной намагниченности, позволяющих определить перемещения по палеошироте, азимутальные повороты, а также изгиб линейных систем и поясов с образованием так называемых ороклиналей; данных о полосовых магнитных аномалиях, по которым, как было показано в предыдущей главе, решаются задачи о конечных движениях литосферных плит и микроплит. Точность палинспастических реконструкций зависит от количества и качества исходных данных. Во многих случаях удается восстановить только приблизительное взаиморасположение объектов, а для многих из них, особенно древних, реконструкции все еще невозможны.
Таким образом, только в стабильных внутриплитных областях для палеотектонической карты может быть использована обычная топографическая основа. Во всех остальных случаях такую карту рисуют на специально созданной палинспастической основе (см.рис.5).
Другая сторона работы по созданию палеотектонической карты состоит в определении тектонической природы главных комплексов пород, геодинамической обстановки их формирования. Эта задача решается на основе актуалистического подхода с учетом характерных ("индикаторных") признаков формаций. Особенно большое значение придается седиментологическим признакам осадочных и петролого-геохимическим признакам магматических пород. Распознаются комплексы континентов: внутриплитные, континентальных рифтов, коллизионных орогенов; комплексы переходных зон континент/океан; пассивных окраин (шельфа, континентального склона и его подножья), активных окраин андского типа, энсиалических и энсиматических островных дуг, преддуговых, задуговых и междуговых бассейнов; коммплексы океанов и микроокеанов: зон спрединга, "вулканических гор", асейсмичных хребтов (в том числе вулканиты "горячих точек"), микроконтинентов. * Многие из этих структурных единиц выделяются и на тектонических картах там, где они развиваются в настоящее время, т.е. в современных зонах перехода континент/океан и в океанских бассейнах.Соответствующие структурные единицы и наиболее важные формации изображаются на палеотектонической карте*. Выявляются и другие, самые разнообразные элементы палеотектонической реконструкции: размещение прогибов и поднятий, источники и направление сноса обломочного материала, ареалы и пояса вулканизма, крупные конседиментационные сбросы и сдвиги, оси зон спрединга и трансформные разломы, линии выхода палеозон Беньофа (а иногда и их глубинное положение в изолиниях), аккреционные призмы, области обдукции офиолитов, главные надвиги зон коллизии. Примером подобных реконструкций может служить серия палеотектонических карт пояса Тетис (1987 г. под редакцией Ж.Деркура и др.), атлас палеотектонических карт Гондваны (1987 г. под редакцией Н.А.Божко и В.Е.Хаина).